Предмет: Математика,
автор: popka5146
Помогите поооожалуйста
Приложения:

Ответы
Автор ответа:
1
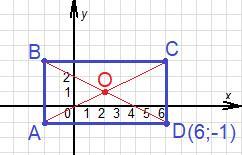
Дан прямоугольник ABCD, A(-2;-1), B(-2;3), C(6,3).
Координаты любой точки в декартовой системе координат задаются в следующем порядке: первая абсцисса (координата х), вторая ордината (координата у).
По рисунку видно, что абсцисса точки D равна абсциссе точки С, а ордината точки D равна ординате точки А.
D(6;-1)
Диагонали прямоугольника точкой пересечения делятся пополам. Найдем координаты середины отрезка AC.
Диагонали прямоугольника AC и BD пересекаются в точке О(2;1).
Ответ: D(6;-1), O(2;1).
Приложения:
Похожие вопросы
Предмет: История,
автор: IngaSanaya
Предмет: Окружающий мир,
автор: ВикторияБеляева
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: fedoseenkoliza
Предмет: Английский язык,
автор: Nargisa12