Предмет: Математика,
автор: antonsiblin
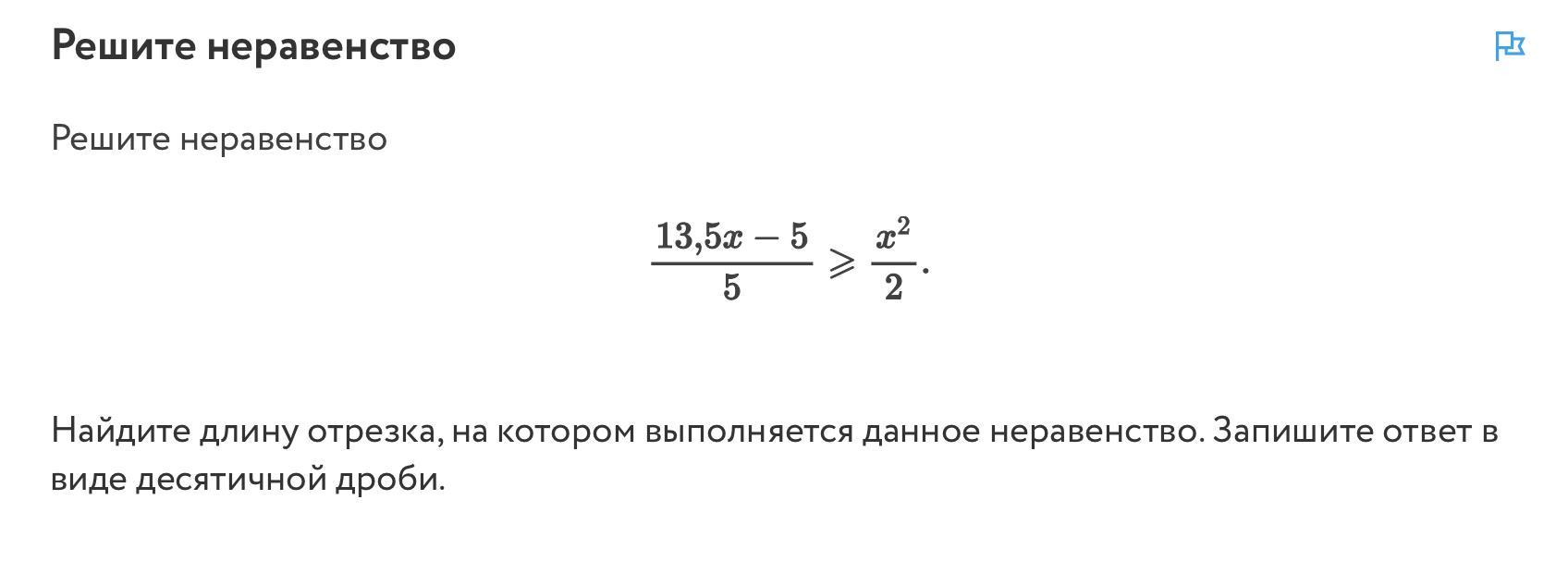
Срочно, пожалуйста !
Приложения:
Ответы
Автор ответа:
0
Находим нули квадратного трёхчлена.
График квадратичной функции - парабола, ветви которой направлены вниз (
). Точки пересечения параболы с осью Ox:
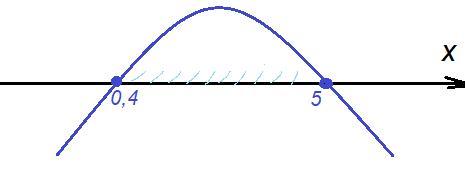
Неравенству удовлетворяет часть параболы над осью Ох (см. приложение).
Длина отрезка:
Ответ: 4,6.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Zak0201
Предмет: Математика,
автор: V9122999966
Предмет: Математика,
автор: 12345702
Предмет: Английский язык,
автор: DKrist
Предмет: Математика,
автор: xXD4GGYXx