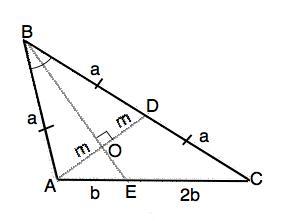
В треугольнике АВС медиана AD и биссектриса ВЕ пересекаются в точке О. Найдите площадь треугольника АВС, если угол АОВ равен 90 градусов, а площадь треугольника АОЕ равна 2.
Ответы
Ответ: 24 (ед. площади)
Объяснение (подробно):
В ∆ АВD биссектриса ВО перпендикулярна стороне АD, ⇒ ВО - высота ∆ АВD. Если биссектриса треугольника еще и высота, этот треугольник - равнобедренный. ВА=ВD, АО=ОD.
Примем АВ=а, тогда ВС=2а, т.к. ВD=DC.
Примем АО=ОD=m
Биссектриса угла треугольника делит противоположную сторону в отношении сторон, заключающих этот угол.⇒
AE:EС=АВ:ВС=1:2.
Пусть АЕ=b, ЕС=2b.
Рассмотрим ∆ АDC и ∆ АОЕ. Они имеют общий угол А.
Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, заключающих равные углы.
Ѕ(АОЕ)=m•b
S(ADE)=2m•3b =>
Ѕ(АОЕ):S(ADE)=mb:6mb=1/6 ⇒
S(ADK)=6•S(AOE)=6•2=12
Медиана делит треугольник на два равновеликих.
S(ABD)=S(ADC).
Ѕ(АВС)=2Ѕ(АDK)=2•12=24 (ед. площади)