Question

ABC - равнобедренный треугольник с основанием AC=25,2. Радиус окружности, вписанной в треугольник ABC равен 4,2. Найдите радиус окружности с центром вне этого треугольника, которая касается продолжений боковых сторон треугольника и касается основания AC.
Пожалуйста, помогите!!!

Answer 1

Ответ:   R=37,8 .

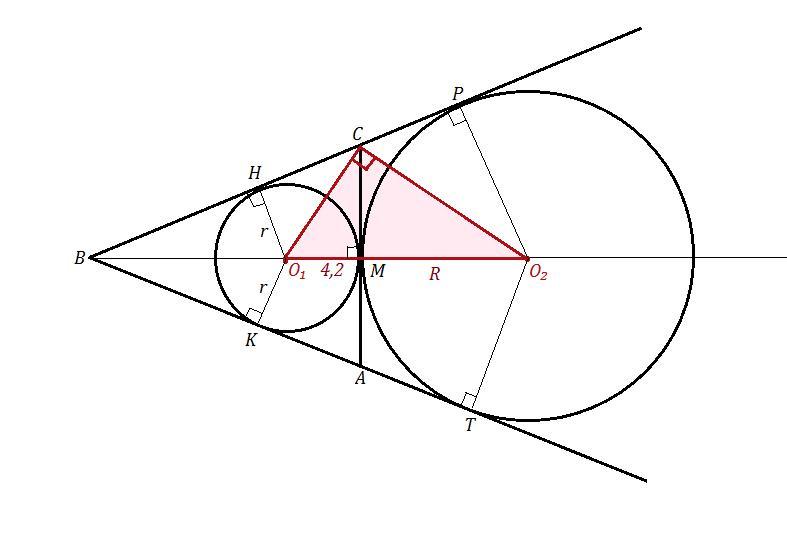
ΔABC ,  AB=BC , AC=25,2  , r= О₁M=O₁H=O₁K=4,2 - радиус вписанной окружности, О₂ - центр вневписанной окружности, которая касается стороны АС и продолжения сторон АВ и ВС , обозначим её радиус через R=О₂М .

Центры О₁ и О₂ лежат на пересечении биссектрис углов треугольника АВС и внешних углов этого треугольника .

О₁С - биссектриса ∠АСВ , О₂С - биссектриса ∠АСР .

Угол между биссектрисами О₁С и О₂С равен 90° , так как

∠АСВ+∠АСР=180° ,  ∠О₁СО₂=∠О₁СА+∠АСО₂=0,5*∠АСВ+0,5*∠АСР=

                                    =0,5(∠АСВ+∠АСР)=0,5*180⁰=90⁰

Рассм. прямоугольный ΔО₁СО₂ , СМ⊥О₁О₂ , так как BМ⊥АС ( BМ - высота, медиана и биссектриса равнобедренного ΔАВС ) ,

АМ=CM=0,5*АС=0,5*25,2=12,6

По свойству высоты прямоугольного треугольника, опущенного из прямого угла на гипотенузу, имеем

 СМ²=О₁М*О₂М  , СМ²=О₁М*R  ⇒  12,6²=4,2*R  ,  R=12,6²:4,2=37,8

Answer 2

Ответ: R = 37,8

Объяснение:

Хотел через подобие, потом раздумал, есть же свойство высоты, проведенной из вершины прямого угла к гипотенузе:

Высота равняется среднему геометрическому отрезков, на которые делит гипотенузу.

То есть $CH=\sqrt{MH*KH}$

Или возводя в квадрат

$CH^2 = MH*KH$