Предмет: Алгебра,
автор: vladimirovleonid88
Решите вот это вот пожалуйста!!!!!!!!
Приложения:
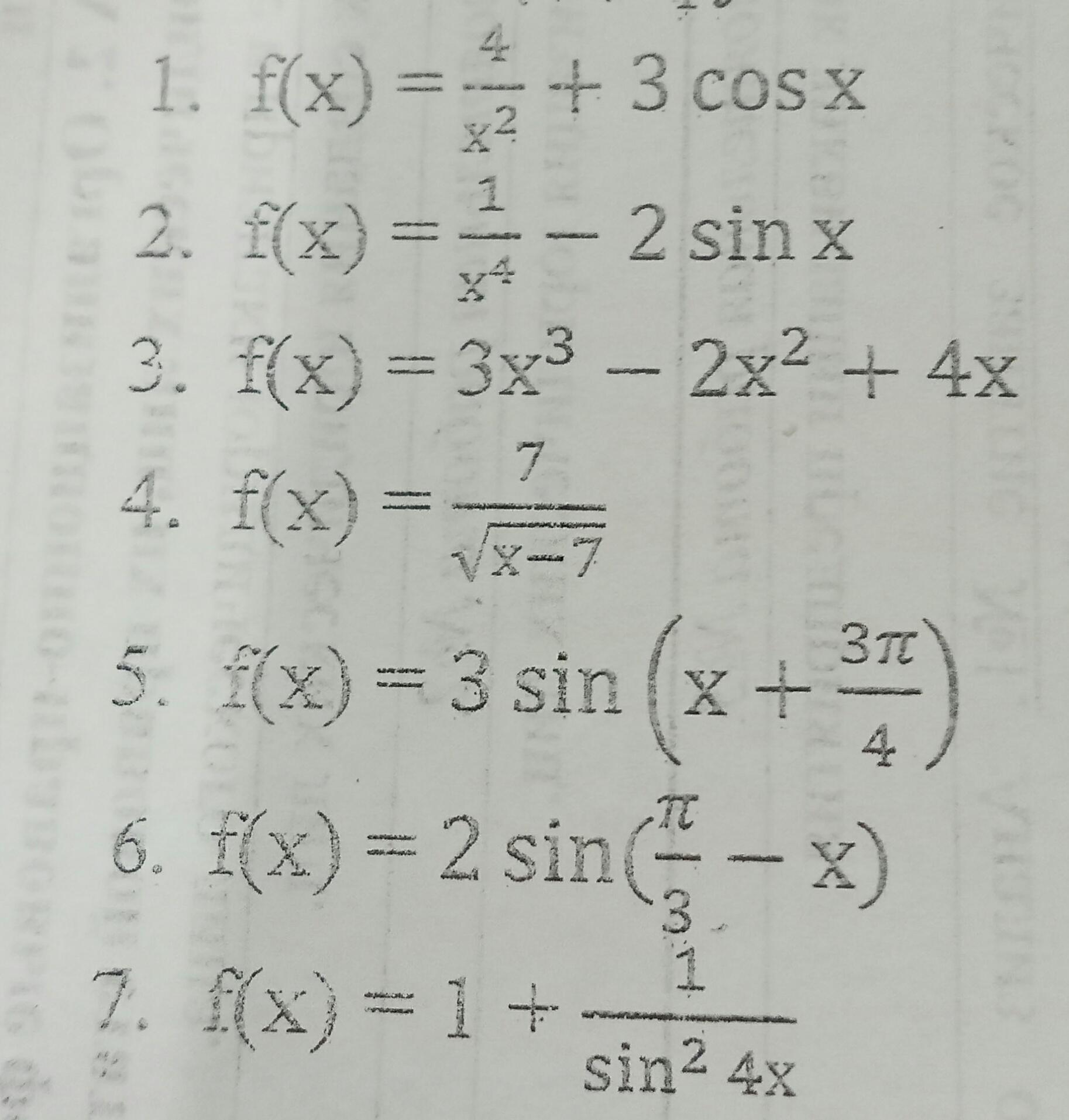
Miroslava227:
производная?
??
Да
Ответы
Автор ответа:
1
Ответ:
1.
2.
3.
4.
5.
6.
7.
Похожие вопросы
Предмет: Русский язык,
автор: капатель3
Предмет: Химия,
автор: aleksandar87
Предмет: Литература,
автор: кристик6
Предмет: Русский язык,
автор: УмникRabchik