Предмет: Математика,
автор: lemurity
Вычислить интеграл с пошаговым решением
Приложения:
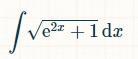
Ответы
Автор ответа:
2
Ответ:
Замена1:
Замена2
Замена3:
Похожие вопросы
Предмет: Окружающий мир,
автор: 6нгр6
Предмет: Химия,
автор: Mashenka551
Предмет: Математика,
автор: настя2151
Предмет: Музыка,
автор: zenkovaK
Предмет: ОБЖ,
автор: msyrtseva2016