Question

Помогите решить дз по геометрии плис! "соотношение между сторонами и углами"

Answer 1

Ответ:

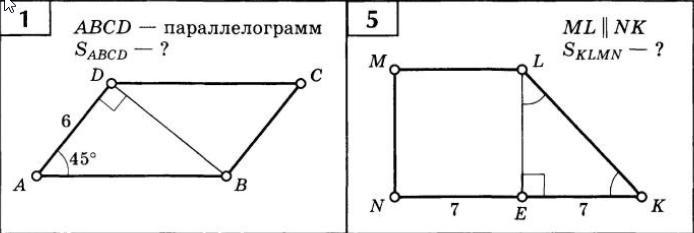
1. Дано:

ABCD - параллелограмм.

∠А=45°

∠D=90°

AD=6

Найти: S(ABCD)

Решение:

1. Рассмотрим ΔADB - прямоугольный. Значит, ∠DBA=90°-45°=45°. Так как ∠DBA=∠DAB=45°, то ΔADB - равнобедренный, отсюда: AD=DB=6 см.

2. Найдем AB в ΔADB по теореме Пифагора:

AB²=AD²+DB²

AB²=6²+6²=36+36=72

AB=√72=√(36*2)=6√2

3. Найдем S(ABCD) по формуле S=a*b*sin∠a

S(ABCD)=AD*AB*sin∠A

S(ABCD)=6*6√2*sin45°=36√2*(√2/2)=(36√2*√2)/2=(36*2)/2=72/2=36

S(ABCD)=36

Ответ: 36

-------------------------------

2. Дано:

ML||NK

∠LEK=90°

∠ELK=∠EKL

NE=EK=7

Найти: S(KLMN)

Решение:

Проведем диагональ NL.

1. Так как в ΔKEL углы равны ∠ELK=∠EKL, то треугольник - равнобедренный, значит EK=EL=7.

Найдем S(ΔKEL) по формуле площади прямоугольного треугольника S=½ab

S(ΔKEL)=½*EL*EK=½*7*7=½*49=24,5

S(ΔKEL)=24,5

2. Рассмотрим ΔNEL и ΔKEL. У них:

• LE - общая сторона

• NE=EK (по условии)

• ∠NEL=∠KEL (смежные углы по 90°)

Значит, ΔNEL=ΔKEL по 2 сторонам и углу между ними.

3. Рассмотрим ΔNEL и ΔLMN. У них:

• NL - общая сторона

• ∠MLN=∠ENL (равны как перекрестные углы при ML||NE и секущей NL)

• ∠LEN=∠MNL=90°

Значит, ΔNEL = ΔLMN по стороне и 2 прилежащим углам.

4. Т.к. ΔNEL=ΔKEL и ΔNEL и ΔLMN, то ΔNEL=ΔKEL=ΔLMN, значит

S(KLMN)=3*S(ΔKEL)=3*24,5=73,5

S(KLMN)=73,5

Ответ: 73,5