Question

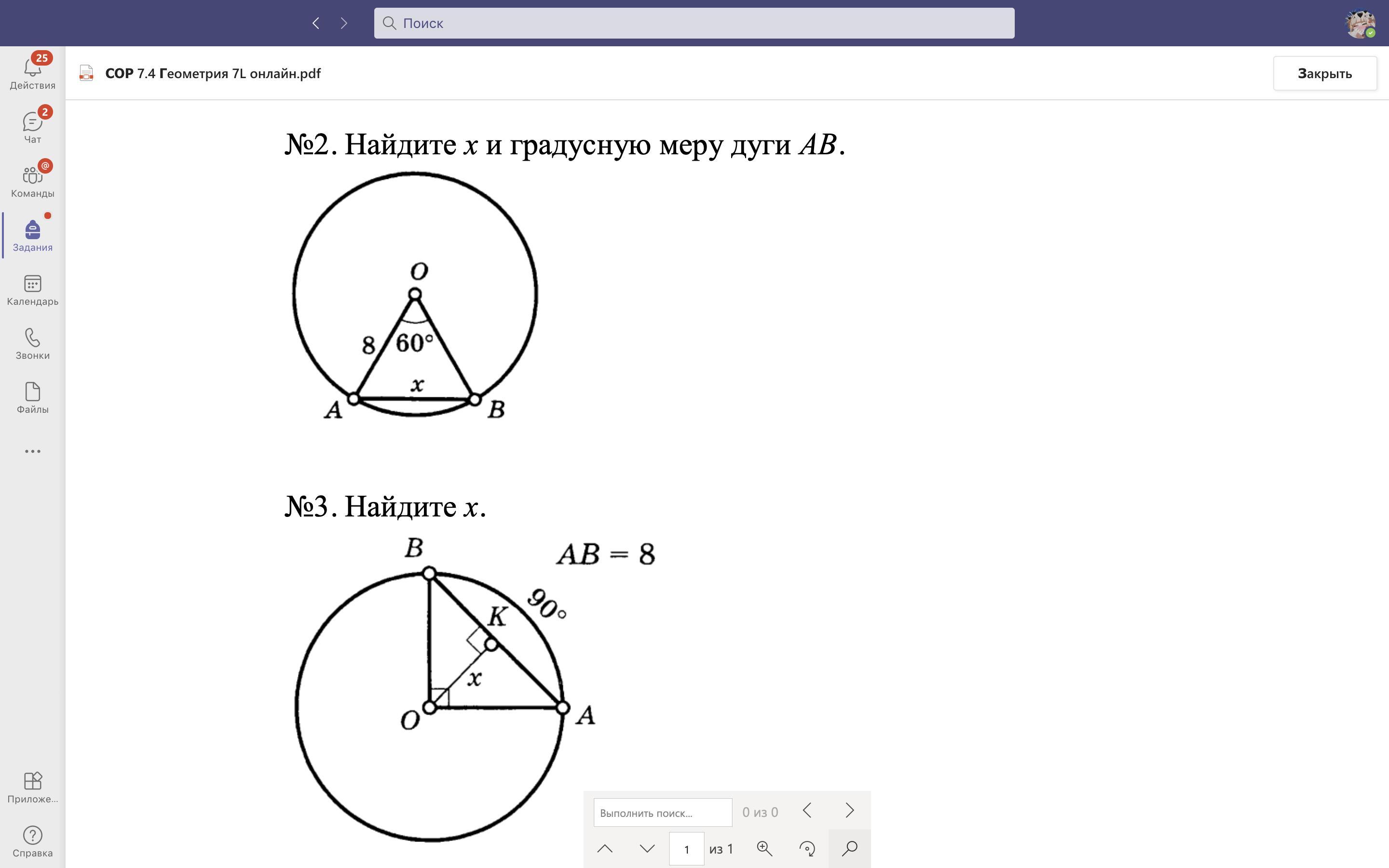
No2. Найдите хи градусную меру дуги АВ.
No3. Найдите х.

Answer 1

Ответ:

2.

Угол АОВ - центральный и опирается на дугу АВ => угол АОВ = дуга АВ = 60°

ОА = ОВ (радиусы) => треугольник АОВ равнобедреннный, но так как один из углов 60°, следовательно два другие тоже по 60°.

Треугольник АОВ - равносторонний.

х = АВ = АО = 8

Ответ: дуга АВ = 60°, х = 8

3.

Треугольник ВОА прямоугольный и равнобедренный (ОВ, ОА - радиусы). Углы ОВА и ОАВ равны по 45°

АВ = 8

$\sin(45^{\circ} ) = \frac{AO}{AB} \\ AO = \frac{ \sqrt{2} }{2} \times 8 = 4 \sqrt{2} \\ \\ \sin(45^{\circ} ) = \frac{KO}{AO} \\ KO = \frac{ \sqrt{2} }{2} \times 4 \sqrt{2} = 2 \times 2 = 4$

Ответ: х = 4

Answer 2

Объяснение:

2) Тк центральный угол 60°, то и дуга на которую он опирается, тоже 60°

3) ∠ВОА=90°, тк опирается на дугу в 90°.

∆ОАВ равнобедренный, тк радиусы ОА ,ОВ равны => ∠В=∠А=45°

Высота ОК является медианой и КА=КВ=4.

∆ОКА равнобедренный тк ∠КОА=90°-45°=45°=∠А=>ОК=КА=4.