Предмет: Алгебра,
автор: Rodik78
Найдите промежутки возрастания и убывания и точки екстремуму функции.
Приложения:
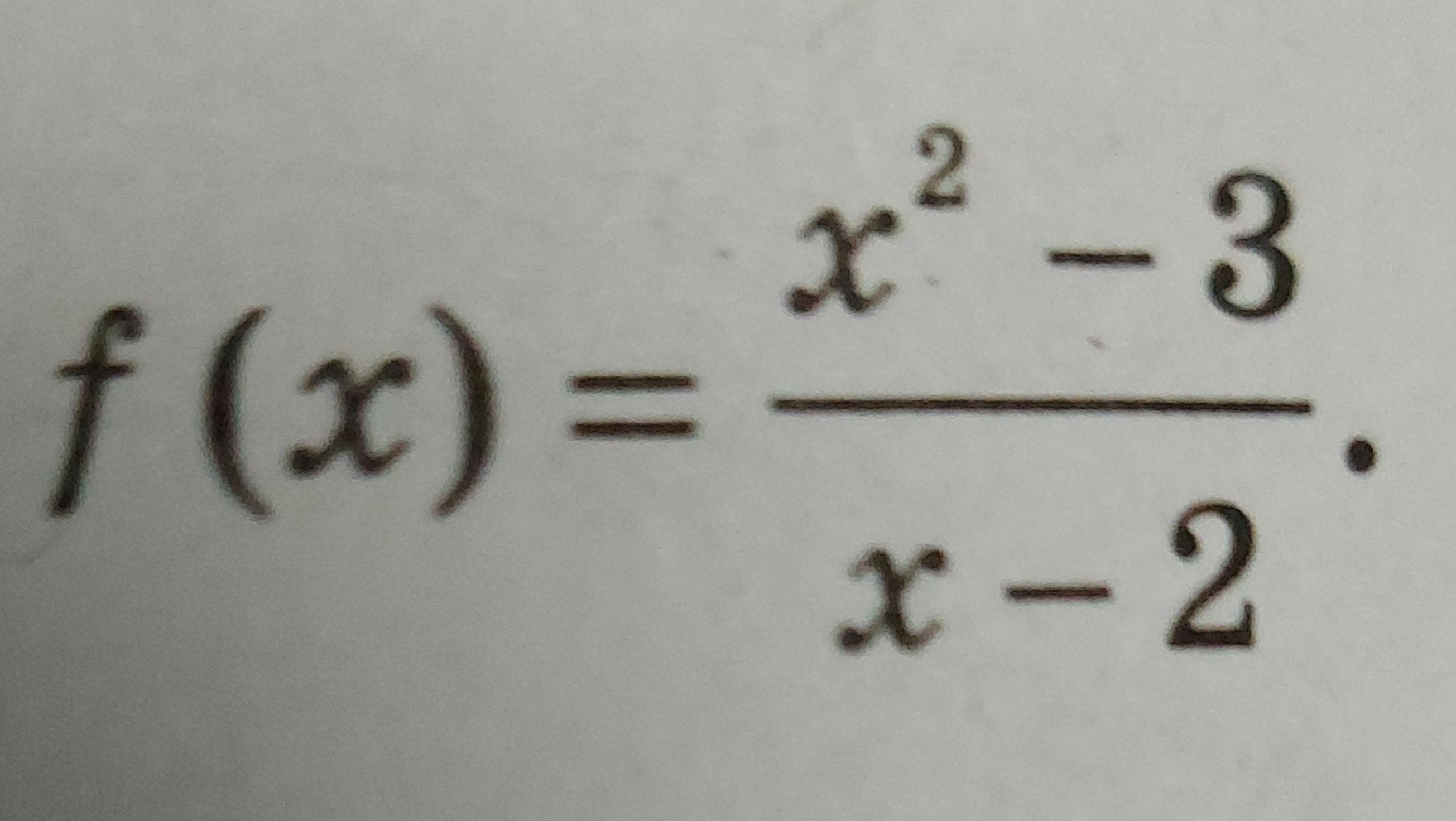
Ответы
Автор ответа:
0
Ответ:
(см. объяснение)
Объяснение:
Возьмем производную от дроби:
Приравняем ее к нулю:
Точки экстремума: 1 и 3.
Критическая точка: 2.
Промежутки возрастания: .
Промежутки убывания: .
Задание выполнено!
Похожие вопросы
Предмет: Русский язык,
автор: милашка58
Предмет: География,
автор: kirillstarchen
Предмет: Русский язык,
автор: pro100albert1kNeO
Предмет: Русский язык,
автор: Ajonber