Предмет: Алгебра,
автор: Sv1narnik
Решите систему уравнений.
В ответ запишите сумму полученной пары чисел.
Приложения:
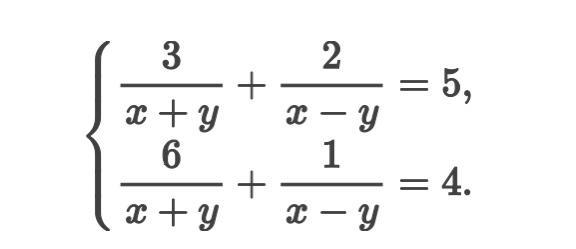
Ответы
Автор ответа:
0
Домножим второе уравнение на 2 и вычтем из первого второе:
x + y = 3 →
Получаем систему (которую решим методом сложения)
у = 3 - 1, 75 = 1,25. Сумма полученной пары = x + y = 3. Ответ: 3
Автор ответа:
1
amanda2sempl:
не тот ответ признали лучшим
Похожие вопросы
Предмет: Литература,
автор: tasyagerasimova
Предмет: Русский язык,
автор: ellissa82
Предмет: Математика,
автор: люба153
Предмет: Математика,
автор: lublupokushat123