Предмет: Математика,
автор: nijomey393
ПРОШУ ПОМОЧЬ, ОЧЕНЬ НУЖНО 35 БАЛЛОВ.
Найти неопределенный интеграл с помощью универсальной
тригонометрической подстановки.
Приложения:
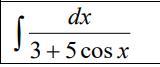
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Биология,
автор: Машуля1004
Предмет: Физика,
автор: физичка2
Предмет: Другие предметы,
автор: Mistela
Предмет: Английский язык,
автор: prematuredeath