Предмет: Алгебра,
автор: gima567
Найдите производную функции
Приложения:
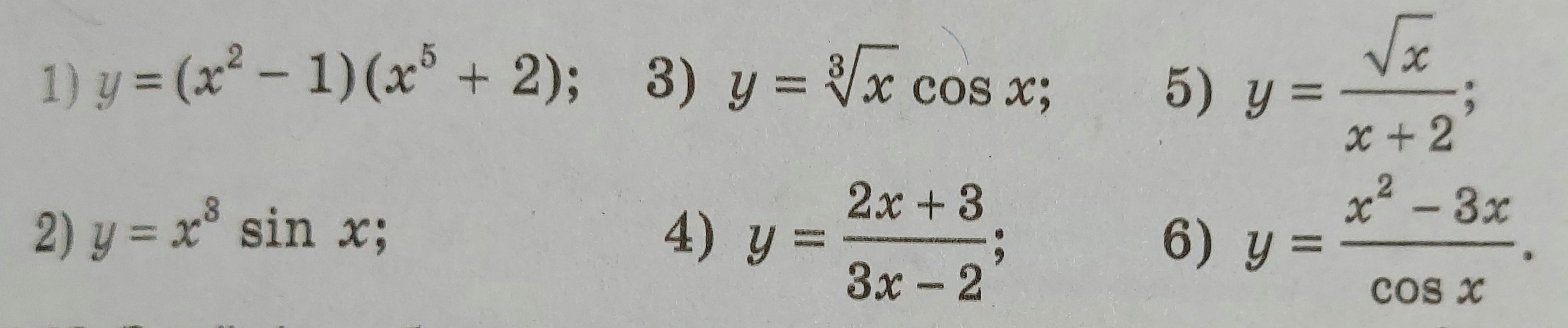
Ответы
Автор ответа:
2
Ответ:
1.
2.
3.
4.
5.
6.
Автор ответа:
1
Решение во вложении, проверяется производная произведения и частного.
Приложения:

Похожие вопросы
Предмет: Окружающий мир,
автор: tan4onok
Предмет: География,
автор: anisimovartem
Предмет: Математика,
автор: Allochka23031983
Предмет: Алгебра,
автор: mashashvedova
Предмет: Английский язык,
автор: unna1