Question

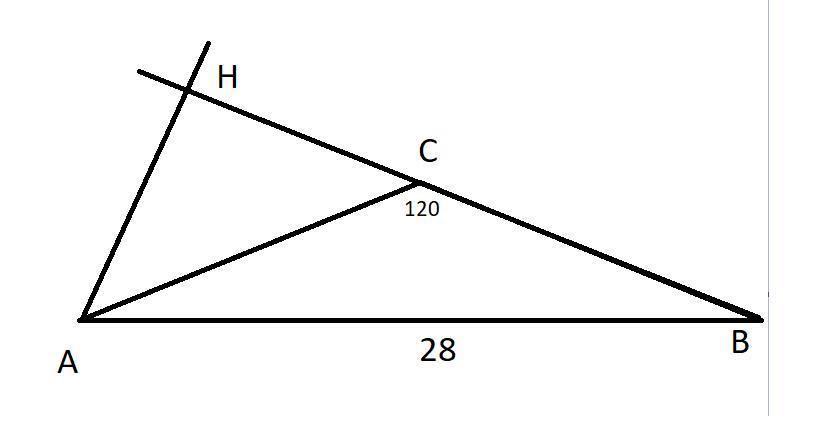
Угол между боковыми сторонами равнобедренного треугольника равен 120°, а основание равно 28 см. Найдите высоту (в см), проведенную к боковой стороне. ПОЖАЛУЙСТА СРОЧНО!!!!

Answer 1

Ответ:

Высота равна 14 см.

Пошаговое объяснение:

Чтобы вычислить длину боковой стороны равнобедренного треугольника, воспользуемся формулой: $a=\frac{b}{2sin\beta/2}$, где a - боковая сторона, b - основание, бета - угол между боковыми сторонами.

$a=\frac{28}{2sin(120/2)}=\frac{28}{2sin60}=\frac{28\sqrt{3} }{3}$

Угол АНС = 90 градусов (так АН - высота), угол СНА = 180-120=60 градусов (так как углы СНА и ВСА смежные), угол НАС = 180-60-90=30 градусов.

Катет, лежащий против угла 30 градусов равен половине гипотенузы, значит СН = 0,5*СА=$0,5*\frac{28\sqrt{3} }{3} =\frac{14\sqrt{3} }{3}$

По теореме Пифагора, АН = $\sqrt{AC^{2}-HC^{2} } =\sqrt{(\frac{28\sqrt{3} }{3})^{2} -(\frac{14\sqrt{3} }{3})^{2} }=14$