Предмет: Алгебра,
автор: nadiy2008
Решите неравенства: фото
Приложения:
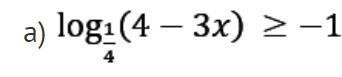
Ответы
Автор ответа:
0
Ответ:
£ - знак "пренадлежит"
x £ [0.
Объяснение:
4-3x
-3x
x
,x<
Автор ответа:
0
ОДЗ :
Похожие вопросы
Предмет: Другие предметы,
автор: катя15197
Предмет: Другие предметы,
автор: Аноним
Предмет: Другие предметы,
автор: Angelinao9
Предмет: Математика,
автор: Какашка78