Question

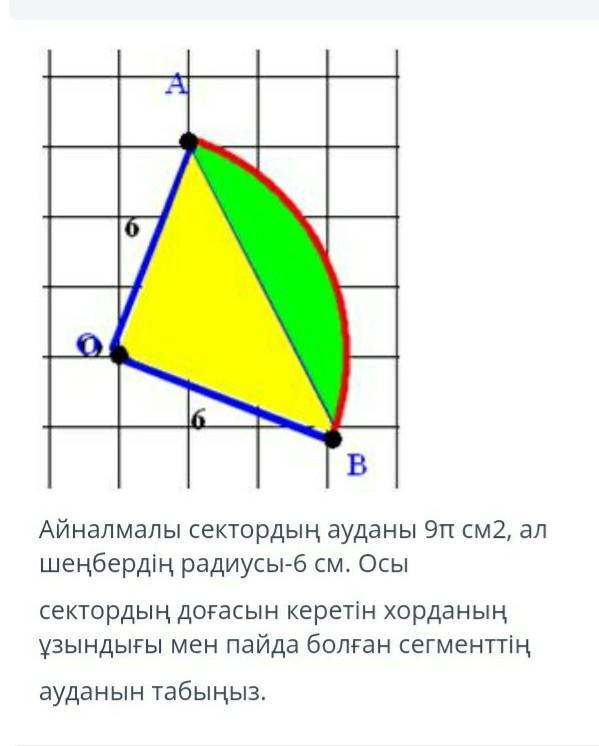
Площадь вращающегося сектора 9 п см2, радиус круга 6 см. Найдите длину хорды, входящей в дугу этого сектора, и площадь полученного отрезка.​

Answer 1

Условие будет звучать по другому:

Площадь кругового сектора равна 9π см² а радиус окружности - 6 см.

Найдите длину хорды стягивающей дугу этого сектора и площадь получившегося сегмента

Решение:

1) Sсектора = $\displaystyle \frac{\pi R^2*\alpha }{360}$

  Scектора= 9π ( по условию ), значит $\displaystyle \frac{\pi R^2*\alpha }{360} =9\pi$

                                                                   $\displaystyle \alpha =\frac{9\pi *360}{\pi R^2}$

                                                                   $\displaystyle \alpha =\frac{9*360}{36}$

                                                                     $\displaystyle \alpha =90$ , т.е ∠АОВ=90°

2) Рассмотрим ΔАОВ: ∠О=90°

   по т.Пифагора АВ²=6²+6²

                              АВ²=72

                              $\displaystyle AB=\sqrt{72} =\sqrt{36*2} =6\sqrt{2}$ - хорда

3) SΔAOB = $\displaystyle \frac{AO*OB}{2} =\frac{6*6}{2} =18$ (см²)

4) Scегмента = Sсектора-SΔ=9π-18=9(π-2)

Ответ: 6√2 ; 9(π-2)