Предмет: Алгебра,
автор: hhhhgj33333
Срочно помогитеее мне пж с решением
Приложения:
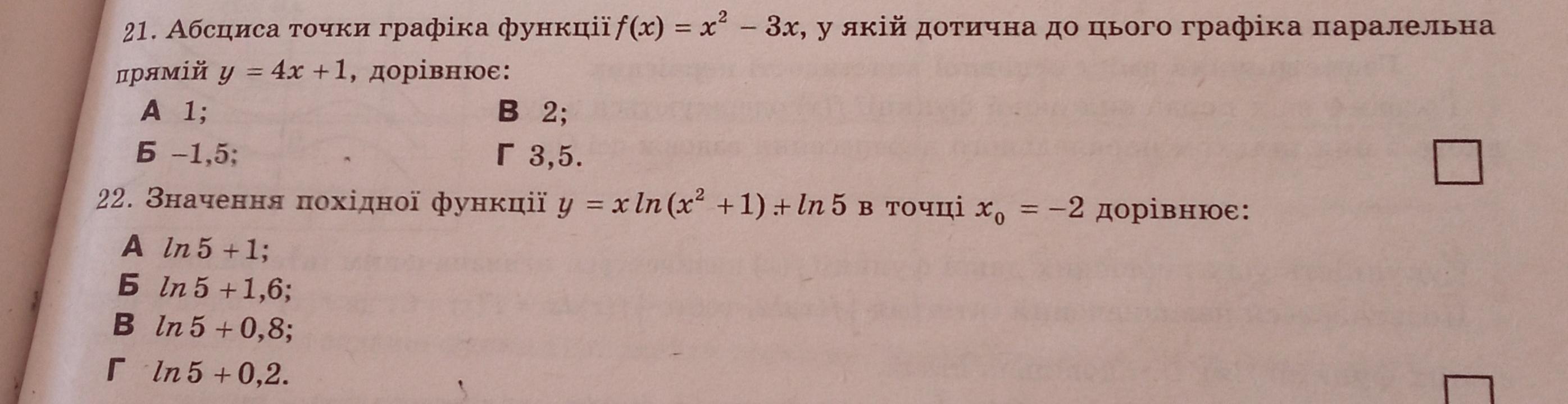
Ответы
Автор ответа:
0
Объяснение:
21.
Пусть абсцисса точки касания графика с касательной равна z. ⇒
Ответ: Г 3,5.
22.
Ответ: Б ln5+1,6.
Похожие вопросы
Предмет: Английский язык,
автор: ELINA042610
Предмет: Окружающий мир,
автор: shomi4ksssssssss
Предмет: Английский язык,
автор: dolgovaeg9
Предмет: Экономика,
автор: kirillka2111
Предмет: Математика,
автор: amku041