Question

ОБЪЯСНИТЕ ЭТАПЫ РЕШЕНИЯ ПОДОБНЫХ ЗАДАНИЙ вычислите площадь фигуры ограниченной линиями y=1+x^3 y=0 x=2

Answer 1

Ответ:

$S = 6,75$

Пошаговое объяснение:

Дано:

$y=1+x^3; \: \: y=0 ; \: \: x=2$

Фигура будет определена, в основном, функцией

$y=1+x^3$

Нам надо найти площадь т.н криволинейной трапеции. Как правило рисунок такой трапеции - это участок под основным графиком,

- сверху фигура ограничена графиком основной функции

- снизу границей является ось Ох

(именно она нам задана в виде функции у=0)

Теперь надо найти ограничения справа и слева. Это могут быть:

- графики функций типа х = a

(вертикальная прямая, пересек. Ох в точке а)

- место пересечения основной функции с осью Ох.

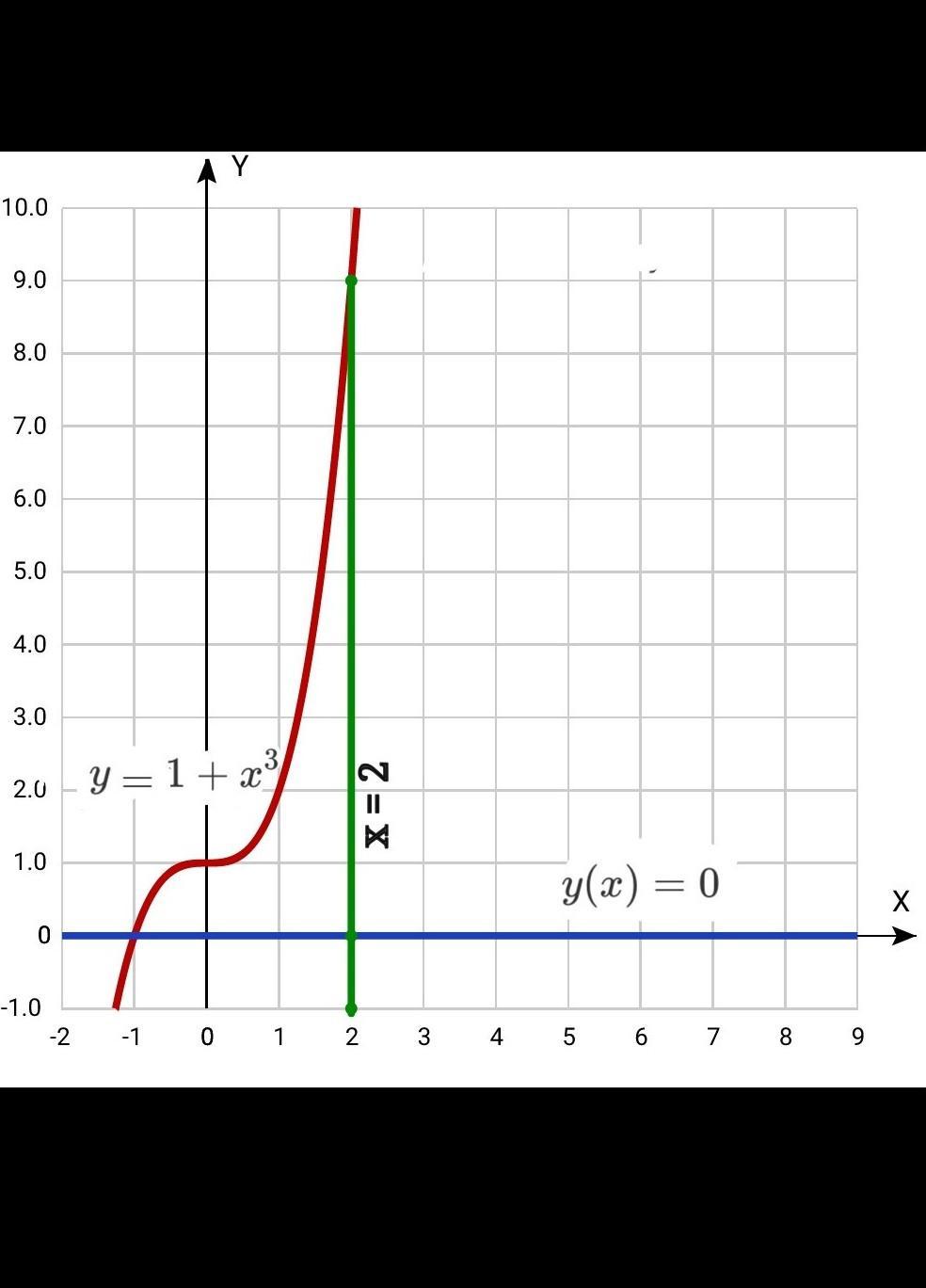
Построим заданные 3 графика (см. рисунок)

Функции у= 0; х=2 - задают ограничения снизу и справа. Слева же график ф-ии

$y=1+x^3$

пересекает Ох в точке (-1;0)

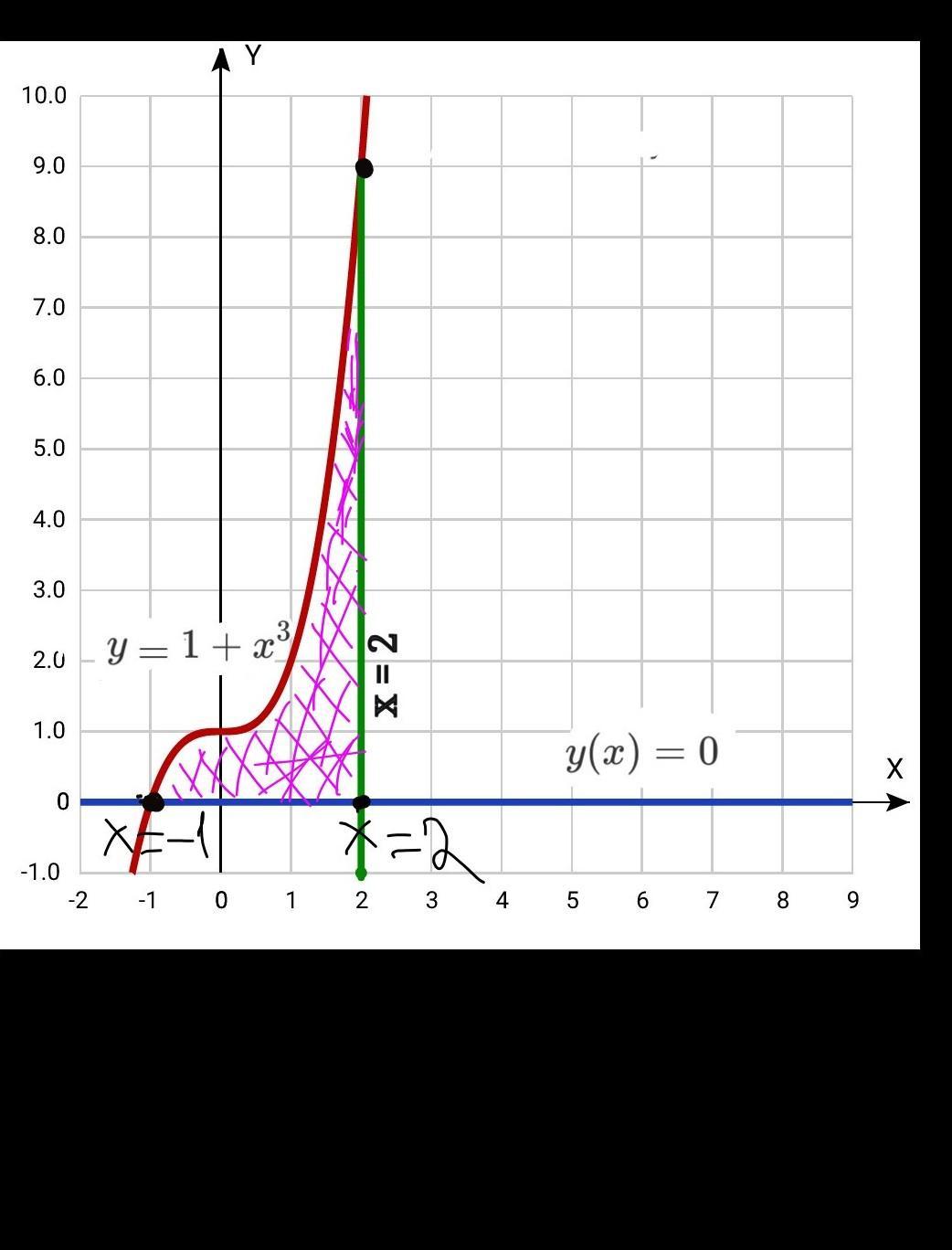
Следовательно, нам необходимо найти площадь фигуры под графиком

$y=1+x^3,$

протянувшуюся вдоль оси Ох от х=(-1) до х=2

(см. второй рис.) Для наглядности на рис. заштриховал нужную фигуру (внезапно!) розовым цветом.

А такие площади находятся при помощи определенного интеграла, причем пределы интегрирования - те самые значения:

от х=(-1) до х=2.

Запишем:

$S = \int\limits_{-1}^{2}(1 + {x}^{3} )dx$

И решим:

$S = \int\limits_{-1}^{2}(1 + {x}^{3} )dx \: = \int\limits_{-1}^{2}dx + \int\limits_{-1}^{2}{x}^{3} dx = \\ = {(}x + \tfrac{ {x}^{4} }{4} {)} \bigg|_{{-}1}^{ \: 2} {=} (2{ +} \tfrac{ {2}^{4} }{4}) - \big(( {-} 1){ + } \tfrac{ {({ - }1)}^{4} }{4} \big) = \\ = \big(2 {+ } \frac{16}{4} \big) - \big( \frac{1}{4} { - }1 \big) = 2 + 4 + \frac{3}{4} = \\ = 6 \frac{3}{4} = 6,75$

Это и будет ответом в задании

Ответ: S = 6,75