Предмет: Математика,
автор: step31121981
Прошу Вас помогите пожалуйста с математикой. Нужна помощь с 4,5,6 заданием. Совсем не идёт. Заранее благодарю
Приложения:
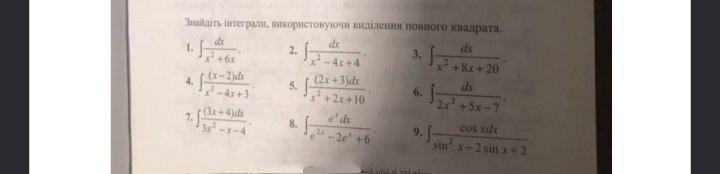
Ответы
Автор ответа:
2
Ответ:
4.
Производную знаменателя (2х-4) делаем в числителе
5.
Делаем в числителе производную знаменателя (2х+2)
Во втором интеграле нужно в знаменателе выделить квадрат суммы
6.
Выделяем квадрат суммы
step31121981:
Спасибо вам огромное!!!
Автор ответа:
1
решения и пояснения к нему во вложении
обычно интегралы, содержащие квадратный трехчлен в знаменателе, берут по алгоритму. 1) находят производную от знаменателя, потом пытаются представить числитель через эту производную, и иногда делают еще и третий шаг- выделяют квадрат суммы или разности двух выражений из знаменателя; эти действия всегда приводят вас к табличным интегралам.
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: Регинка10
Предмет: Русский язык,
автор: Oxygun11
Предмет: Математика,
автор: mindarina2