даю 15 баллов.С объяснением)
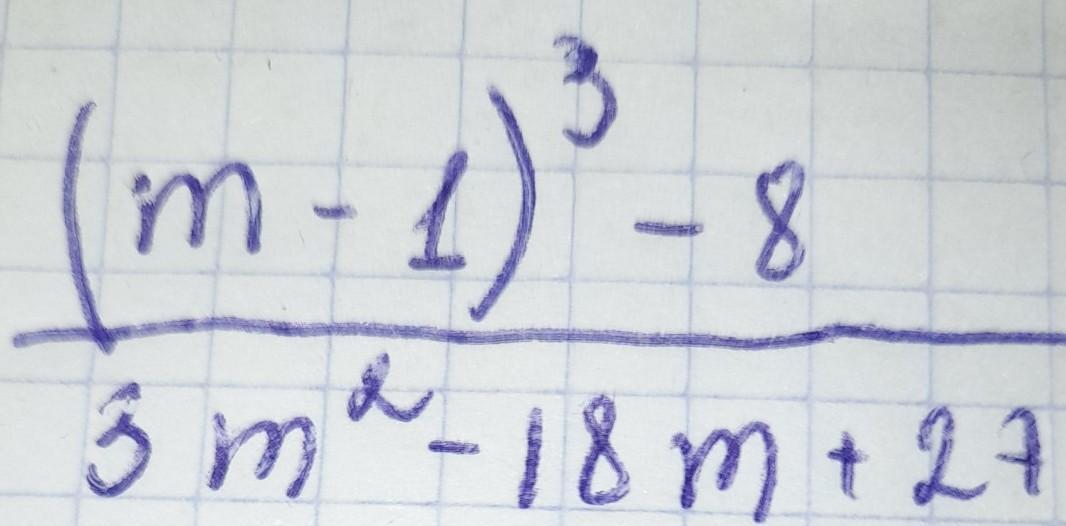
Ответы
Ответ:
в числителе формула х³-у³=(х-у)(х²+ху+у²) в качестве х берем (m-1), а у- это 2, т.к. 8=2³
в знаменателе можно вынести за скобку общий множитель 3, получим
3*(m²-6m+9)=3*(m-3)²- здесь использовали формулу, по которой свернули х²-2ху+у²=(х-у)², теперь х- это m, а у -это 3, вот посмотрите.
m²-6m+9=m²-2*m*3+3³
похожа запись на формулу х²-2ху+у²? Просто их там несколько формул сокращенного умножения, чтобы с ними разобраться, их надо выучить. ну или иметь постоянно под рукой. т.к. они теперь Вас постоянно будут преследовать. пока Вы учите алгебру..
Теперь, что же получим, преобразовав числитель и знаменатель?
((m-1-2)*((m-1)²+(m-1)*2+4)/(3*(m-3)²)=
((m-3)*((m²-2m+1+2m-2+4)/(3*(m-3)²)=((m²-2m+1+2m-2+4)/(3*(m-3))=
(m²+3)/(3*(m-3)=(m²+3)/(3*m-9)
УДАЧИ.