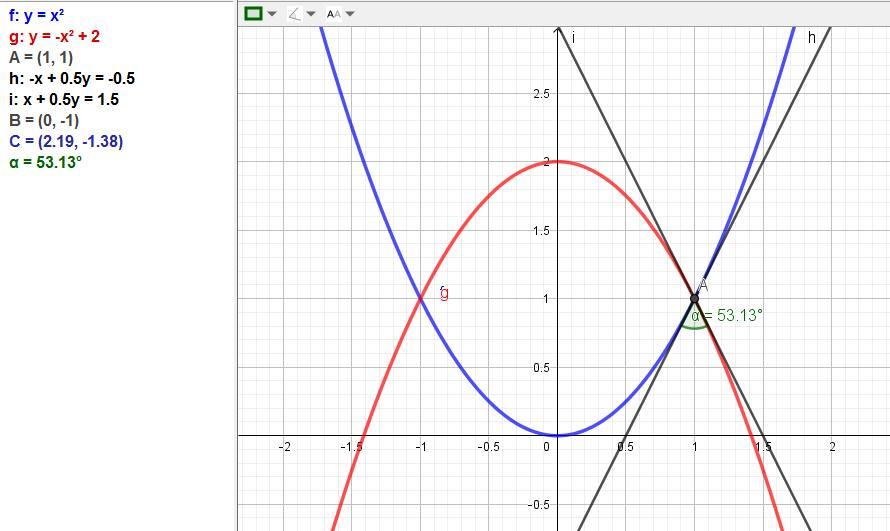
Найти острый угол между параболами y=x^2 y=2-x^2 в той точке их пересечения, которая имеет положительную абсциссу
Ответы
Находим точку пересечения.
x^2 =2-x^2,
2x^2 =2,
х = +-1.
Принимаем по заданию точку пересечения, которая имеет положительную абсциссу. Это точка А(1; 1).
Угол наклона касательной к оси Ох равен производной функции в точке касания.
y = x^2 y' = 2x⇒ x= 1 ⇒ y' = 2.
y=2-x^2, y' = -2x ⇒ x= 1 ⇒ y' = -2.
Отсюда видно, что касательные симметричны относительно вертикальной линии, проходящей через точку их пересечения.
Ответ: угол равен 2arc tg(1/2) = 53,13 градуса.
Можно искать угол по формуле tg(α+β) = (tgα +tgβ)/(1-tgα*tgβ).
Получим угол -53,13 градуса или 180 - 53,13 = 126,87 это тупой угол по часовой стрелке от касательной с положительным угловым коэффициентом до касательной с отрицательным угловым коэффициентом..
Острый же угол равен полученному по этой формуле по модулю.