Question

Вычислить площадь фигуры ограниченной линиями
y=9-x^2
y=3x+5
С подробным решением
100 баллов

Answer 1

Ответ:

Пошаговое объяснение:

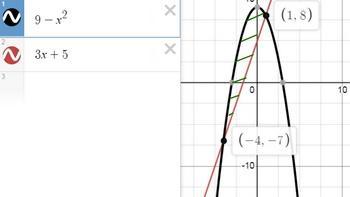
здесь все подробности берутся из чертежа. рисуем нрафики, определяем точки пересечения и полученную фигуру, за у1 берем функцию, график которой располагается "выше", за у2 ту, график котой ниже

общая формула

$\displaystyle S=\int\limits^a_b {(y_1-y_2)} \, dx$

в нашем случае

$\displaystyle S=\int\limits^1_{-4} {((--x^2)-(3x+5))x} \, dx =\int\limits^1_{-4} {(-x^2-3x+4)} \, dx =$

$\displaystyle =\bigg ( -\frac{x^3}{3} -\frac{3x^2}{2} +4x \bigg ) \bigg |_{-4}^1=-\frac{64}{3} +\frac{45}{2} +20=\frac{125}{6}$