Предмет: Математика,
автор: laktina20009
помогите пожалуйста найти производную функции
Приложения:
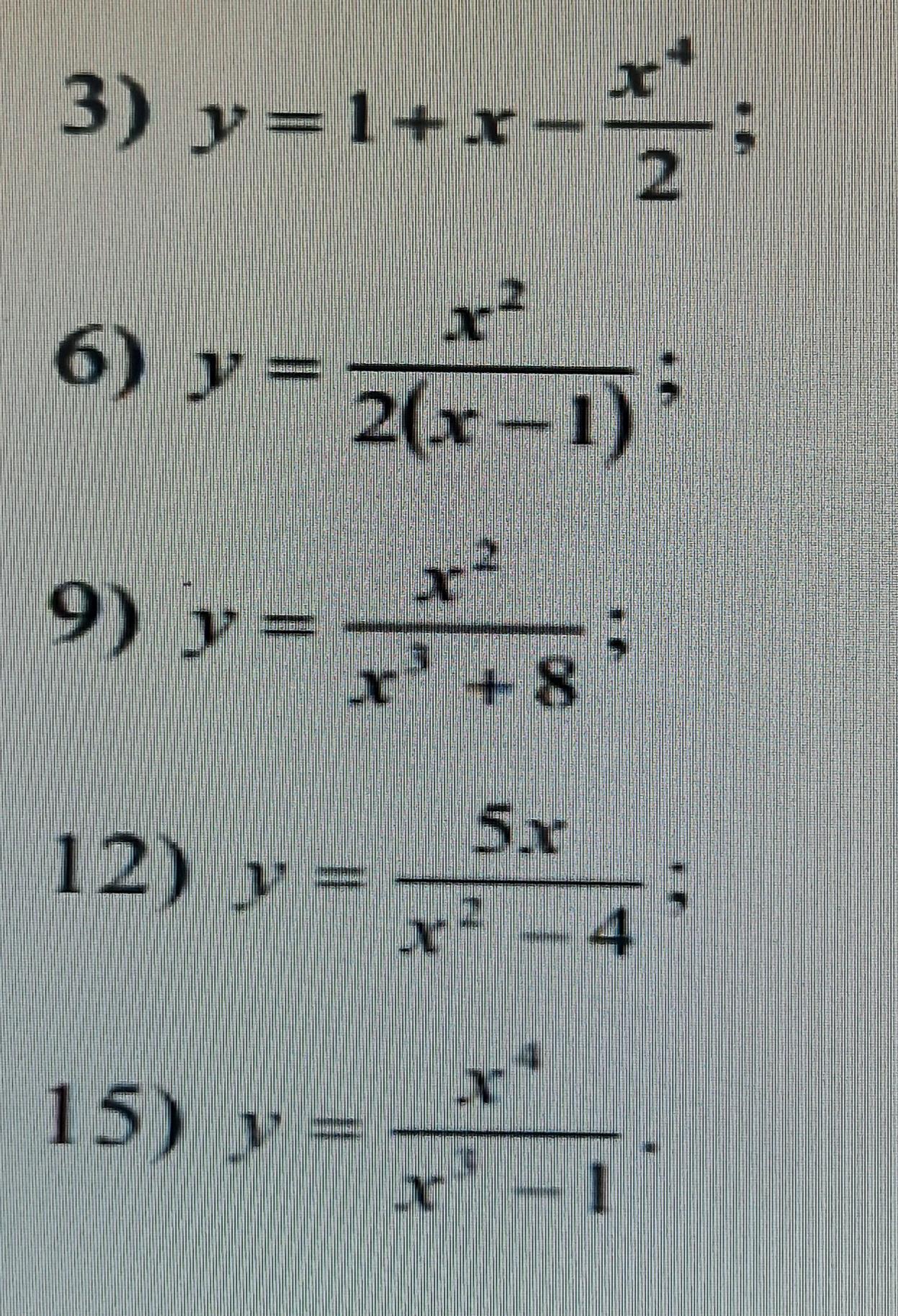
Ответы
Автор ответа:
1
Ответ:
3
6
9
12
15
Похожие вопросы
Предмет: Русский язык,
автор: Чаëк01
Предмет: Қазақ тiлi,
автор: асель26
Предмет: Окружающий мир,
автор: маня133
Предмет: Математика,
автор: Vikakt
Предмет: Химия,
автор: smirnovavasili