Предмет: Математика,
автор: danilpanteleev2012
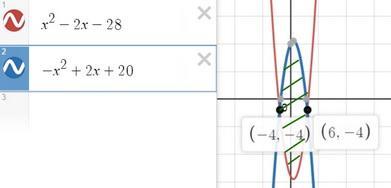
Вычеслите площадь фигуры, ограниченной линиями y=x^2-2x-28,y=2x+20-x^2
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
рисуем графики функций, определяем фигуру и пределы интегрирования
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: знание9
Предмет: Английский язык,
автор: катя2133
Предмет: Английский язык,
автор: spakim
Предмет: Математика,
автор: дима3068
Предмет: Английский язык,
автор: МехрибанЛейсан