Question

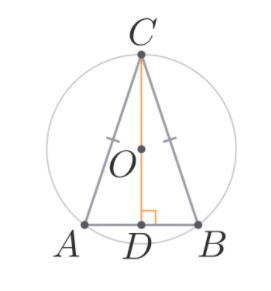
Равнобедренный треугольник ABC (AB=BC) вписан в окружность с центром O.

Известно, что AB=18, DO=12 , где D-основание перпендикуляра из O на AB .

Найдите площадь треугольника .

Answer 1

АD=BD=AB/2=18/2=9, т.к. высота равнобедренного треугольника АВС, проведенная к основанию АВ является и медианой. т.е. делит сторону АВ пополам. Зная

СО=АО=ВО как радиусы описанной окружности. Зная DO и АD, легко найти радиус R=AO=√(AD²+OD²)=√(81+144)=√225=15$

Как известно, по следствию из теоремы синусов, АВ/sin∠C=2R, АВ/sin∠C=2*15⇒sin∠C=18/30=3/5=0.6; cos∠C=±√(1-0.36)=±0.8;

Если угол С тупой, то косинус отрицателен, если острый. то положителен.

2sin²(∠C/2)=1-cos∠C;⇒а)cos∠C=0.8; 2sin²(∠C/2)=1-0.8=0.2; sin²(∠C/2)=0.1; sin(∠C/2)=√0.1;

б) Если же сos∠C=-0.8; 2sin²(∠C/2)=1+0.8=1.8; sin²(∠C/2)=0.9; sin(∠C/2)=√0.9;

Зная синус угла ВСD, можно найти гипотенузу СВ из прямоугольного треугольника ВСD; СВ=DB/sin∠ВСD=9/√0.1, или 9/√0.9;

а зная две стороны и угол между ними можно найти площадь треугольника. Она равна (СВ²*sin∠C)/2=(81/0.1)*0.6/2=243 или

(81/0.9)*0.6/2=27