Какие НЕВЕРНЫ?
1. Длина окружности больше её диаметра в «пи» раз.
2. Если два вписанных в окружность угла опираются на одну и ту же дугу, то они равны.
3. Любой четырёхугольник можно вписать в окружность.
4. Если взять точку, лежащую вне окружности, и провести от неё две касательных к этой окружности, то отрезки от этой точки до точек касания будут равны.
Ответы
1. Длина окружности больше её диаметра в «пи» раз - верно, т.к. одна из формул для нахждения длины окружности C = πD, где С - длина окружности, D - диаметр, т.е. действительно длина окружности больше её диаметра в «пи» раз.
2. Если два вписанных в окружность угла опираются на одну и ту же дугу, то они равны - верно, есть теорема: если вписанные углы опираются на одну дугу, то они равны.
3. Любой четырёхугольник можно вписать в окружность - неверно, т.к. есть теорема: если сумма противоположных углов четырехугольника равна 180°, то его можно вписать в окружность. Таким образом, в окружность можно вписать (из изученых четырехугольников) квадрат, прямоугольник и равнобокую трапецию.
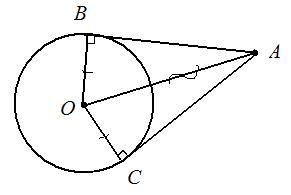
4. Если взять точку, лежащую вне окружности, и провести от неё две касательных к этой окружности, то отрезки от этой точки до точек касания будут равны - верно, т.к. есть соответствующая теорема (см. рис.).
По рисунку видно, что прямоугольные треугольники АОВ и АОС равны по катету ОА = ОВ (радиусы) и гипотенузе (АО - общая сторона треугольников), а радиусы, проведенные в точку касания, перпендикулярны касательной.
Ответ: 3.