ДАЮ 35 БАЛЛОВ!!!!!!!!!!!!!!!!!
На примере уравнения(оно в файле) объясните, как решают дробные рациональные уравнения
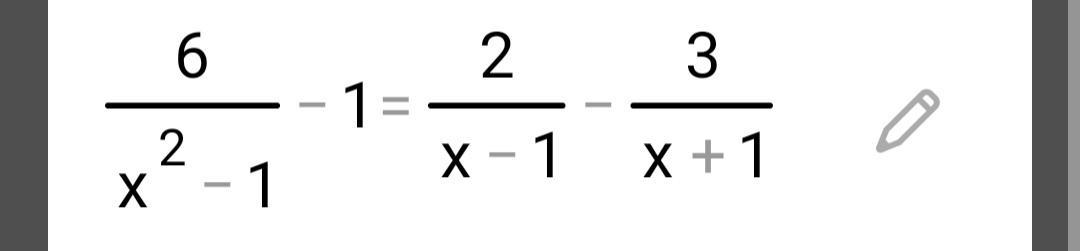
Ответы
Ответ:
↓↓↓
Объяснение:
1 знаменатель раскладывается по формуле разности квадрата (х-1)(х+1)
Тогда общий знаменатель (х-1)(х+1) . И тогда ОДЗ (х-1)(х+1) ≠0⇒х≠1,х≠-1.
Умножим все выражения И ПРАВОЙ И ЛЕВОЙ части на общий знаменатель. Тогда кое-что посокращается и получится новое уравнение без дробей
6-1*(х²-1)=2*(х+1)-3*(х-1)
6-х²+1=2х+2-3х+3
х²-х-2=0 , Д=1+8=9,
х₁=(1-3):2=-1 не подходит под ОДЗ
х₂=(1+3):2=2
Ответ .х=2
Объяснение:
6 - x^2 - 1 т.к. привод. к общ. зн.
x^2 - 1 x^2 - 1
(х^2 - 1 ) раскладываем как (x-1)x(x+1) ; как по формуле
подставляем и получаем:
6 - (x-1)x(x+1)
(x-1)x(x+1)
---------------------------------
далее берем 2 часть уравнения
2 - 3
х-1 х+1
приводим к общему знаменателю (1 часть умножаем на x+1 а вторую на х-1
получаем
2×(х+1) - 3×(х-1)
(х-1)(х+1)
переносим через равно
6 - (x-1)x(x+1) -2×(х+1) +3×(х-1)
_______________________
(x-1)x(x+1)
Х=2