Question

Помогите пожалуйста. Исследуйте функцию с помощью производной и постройте ее график. Даю 40 баллов

Answer 1

Пошаговое объяснение:

а)

$f(x) = \frac{1}{4} {x}^{4} - 3 {x}^{2} + 2$

1 Область определения ф-ии D(f):

D(f) = R - ф-ия определена для любого значения х

2 Четность:

$f( - x) = \frac{1}{4} {( - x)}^{4} - 3 {( - x)}^{2} + 2 = \\ = \frac{1}{4} {x}^{4} - 3 {x}^{2} + 2 = f(x)$

Функция является четной, т.к. f(-x)= f(x)

3 Пересечения с Ох и Оу:

с Оу (х=0):

$f(0) = \frac{1}{4} \cdot {0}^{4} - 3 \cdot{0}^{2} + 2 = 2$

с Ох (у=0):

$f(x) = 0 \\ \frac{1}{4} {x}^{4} - 3 {x}^{2} + 2 = 0 \\ {x}^{4} - 12 {x}^{2} + 8 \\ t = {x}^{2} \geqslant 0 < = > x = \pm \sqrt{t \: } \\ {t}^{2} - 12t + 8 = 0 \\ D/4 = 6^{2} -8 = 32, \\ t = 6±4 \sqrt{2} \\ x = ± \sqrt{6±4 \sqrt{2}}$

Производная

$f'(x) = ( \frac{1}{4} {x}^{4} - 3 {x}^{2} + 2 )'\\ f'(x) = (\frac{1}{4} {x}^{4})' - (3 {x}^{2})' + (2)' = \\ = \frac{1}{4} \cdot4{x}^{3} - 3 \cdot 2{x}^{1} + 0 = {x}^{3} - 6x \\ \\ f'(x) = 0 \: < = > \: {x}^{3} - 6x = 0 \\ x( {x}^{2} - 6) = 0 \\ x( x- \sqrt{6} )(x + \sqrt{6} ) = 0$

$x_1 = - \sqrt{6}; \: x_2 = 0; \: x_3=\sqrt{6} \: \\ x_1 ; \: x_2 ; \: x_3- \text{tt. \: extremuma} \\ f( - \sqrt{6} ) {= } \frac{1}{4}{ \cdot } { ( - \sqrt{6}) }^{4} { -} 3{\cdot} { ( - \sqrt{6}) }^{2} {+ }2 = \\ \frac{ {36} }{4} - 3 \cdot6 + 2 = 9 - 18 + 2 = - 7 \\ f(0) = 2\\ f( \sqrt{6}) = f( - \sqrt{6} ) = - 7$

${-}^{-}{-} _{(-\sqrt{6})} { -} ^{ + }{-}_{(0)}- ^{-} - _{(\sqrt{6})}- ^{ + }{-}$

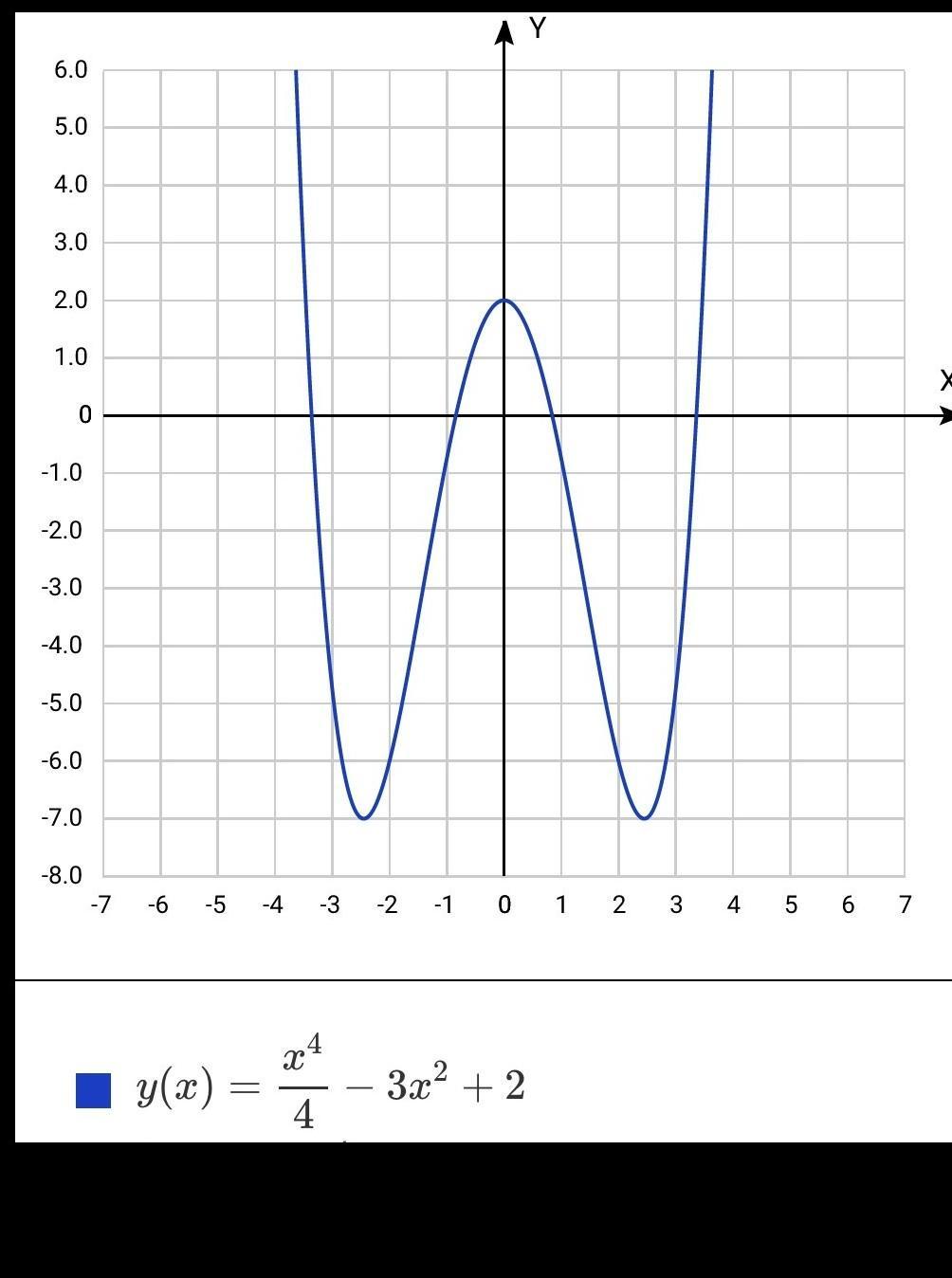
т.е. (-✓6; -7); (✓6; -7) - точки минимума ф-ии

(0; 2) - точка максимума ф-ии.

График ф-ии будет выглядеть так: (см. на рис.)