Предмет: Математика,
автор: 567545676676
Помогите решить СРОЧНО!!! Дам 50 баллов! В 4 и 6 примере, интеграл растянут на всю дробь.
Приложения:
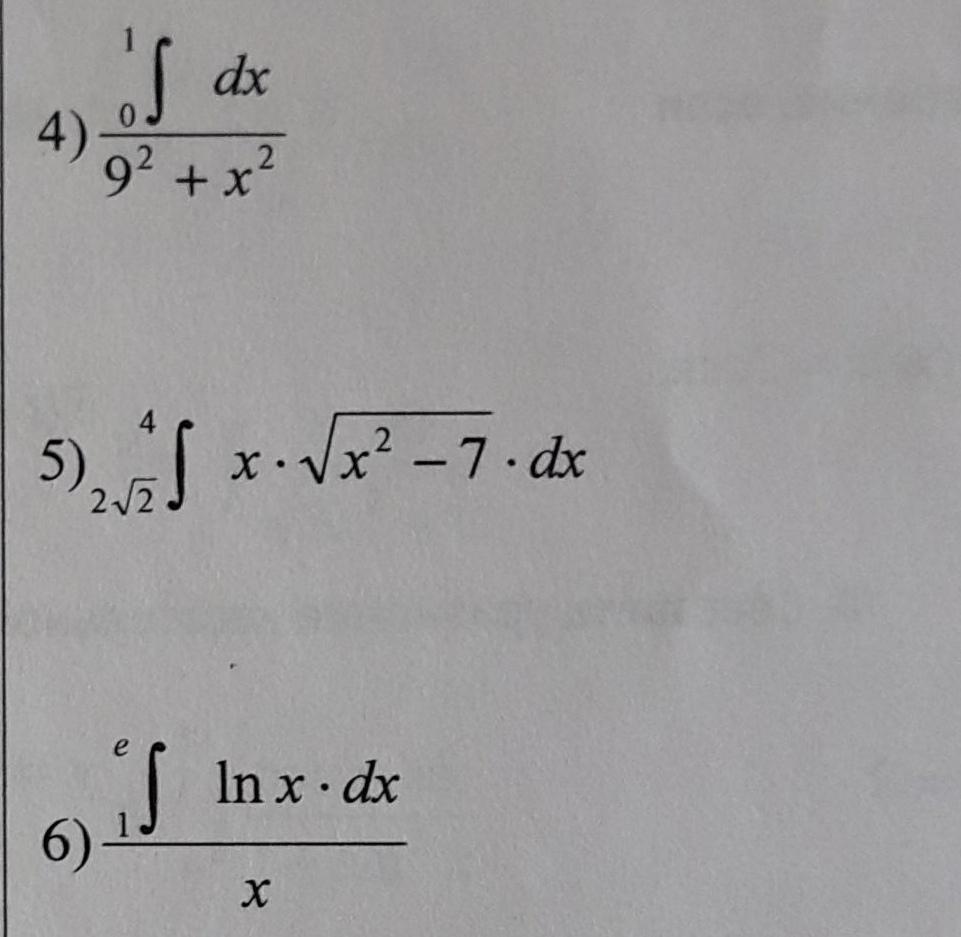
Ответы
Автор ответа:
1
Ответ:
4
5
6
Похожие вопросы
Предмет: Русский язык,
автор: MashaFlower05
Предмет: Русский язык,
автор: сашуля78945
Предмет: Английский язык,
автор: lia0404
Предмет: Английский язык,
автор: ппапор
Предмет: Русский язык,
автор: LiskaKiska224