Question

Даны вершины треугольника АВС А(4,1), В(24), С(0,1). Определите вид треугольника и найдите его периметр.​

Answer 1

Ответ:

2$\sqrt{13}$+4, равнобедренный треугольник

Объяснение:

Можно решать через вектора:

AB = (2-4, 4-1) = (-2,3) Длина AB = корень из ((-2)*(-2)+3*3) = $\sqrt{13}$

CB = (2-0, 1-4) = (2,-3) Длина CB = корень из (2*2+(-3)*(-3)) = $\sqrt{13}$

CA = (4-0,1-1) = (4,0) Длина AC =4

Итого: AB = CB, значит треугольник равнобедренный,

периметр = 2$\sqrt{13}$+4

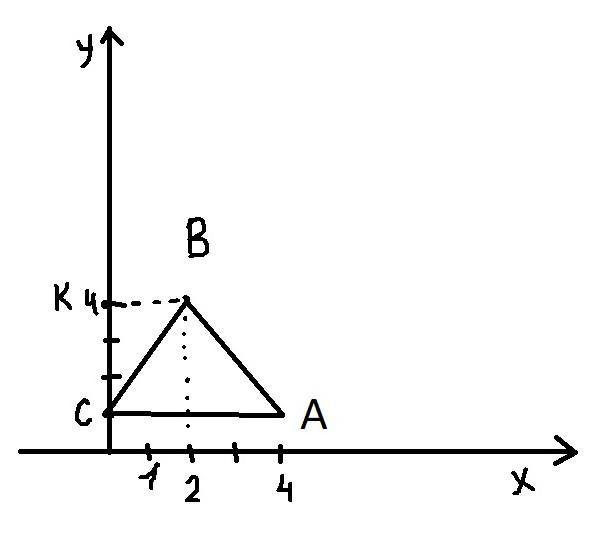
Можно просто через картинку, проведем точку К и найдем CB по теореме Пифагора: CB^2 = KB^2+CK^2 = 2^2+3^2 = 13

Отсюда CB =$\sqrt{13}$

Аналогично AB

CA = 4 из рисунка

периметр = 2$\sqrt{13}$+4