Предмет: Алгебра,
автор: polinashevtsovaaa
Найти производную от частного сложной функции:

Ответы
Автор ответа:
1
Ответ:
Приложения:
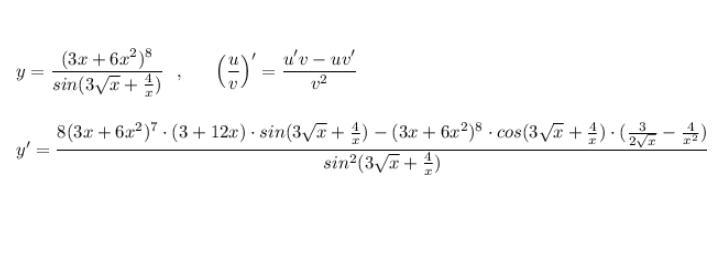
Похожие вопросы
Предмет: Русский язык,
автор: samandra135
Предмет: Русский язык,
автор: marinakot1
Предмет: Английский язык,
автор: LastLove
Предмет: География,
автор: mila17711
Предмет: История,
автор: Lime11111