Предмет: Алгебра,
автор: gogovili
решите деференциальное уравнение и укажите его частное решение, удовлетворяющее начальному условию y(0)=2
Приложения:
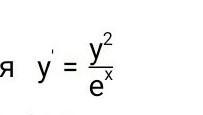
Ответы
Автор ответа:
0
Ответ:
общее решение
частное решение
Похожие вопросы
Предмет: Другие предметы,
автор: andrey2sanna
Предмет: Русский язык,
автор: sasha23ru
Предмет: Русский язык,
автор: АЛЬМУХАНОВА
Предмет: Биология,
автор: Knopa92