Предмет: Алгебра,
автор: jdjdjrbrgrh7273737
Срочноооооооооо ребятааааа помогитеее с полным решением
Приложения:
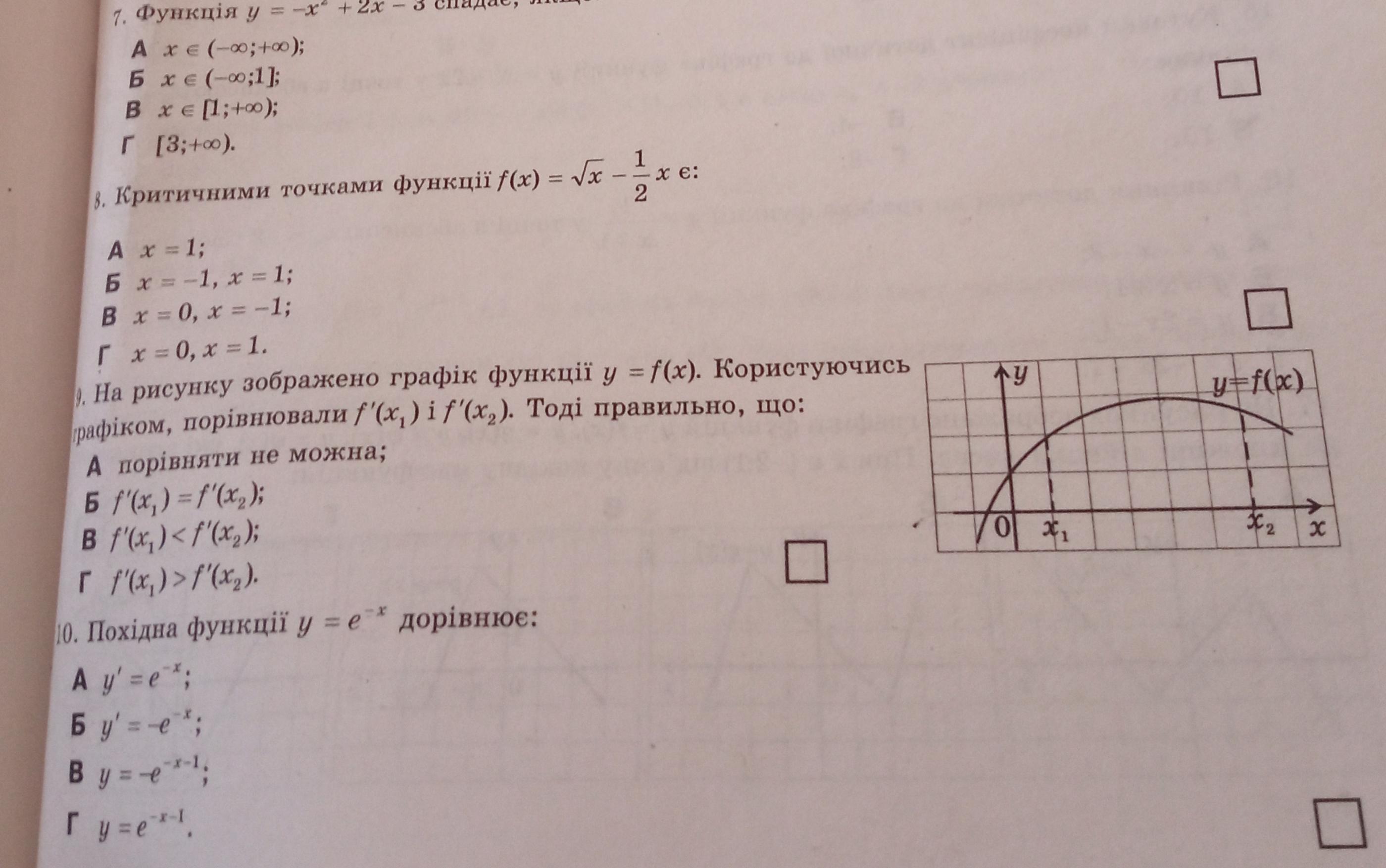
Ответы
Автор ответа:
0
Ответ:
Автор ответа:
0
ответ:
- В
- А
- Г
- Б
объяснение:
Приложения:
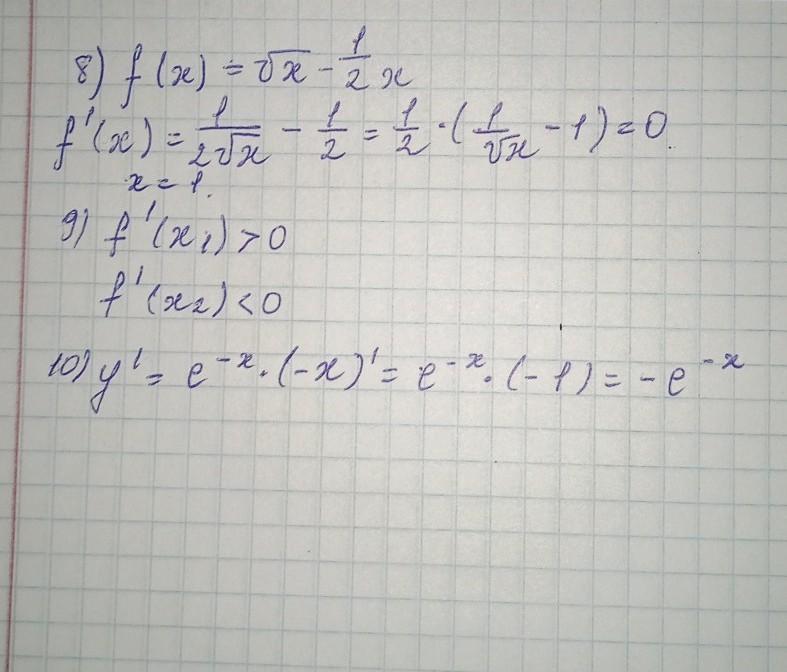
Похожие вопросы
Предмет: Русский язык,
автор: sauleshakss57
Предмет: Окружающий мир,
автор: белый9
Предмет: Русский язык,
автор: rttyu
Предмет: Английский язык,
автор: айя36