Предмет: Алгебра,
автор: undina77
Найти неопределенные интегралы методом замены переменной, с решением пожайлуста.
И прошу не писать просто так, что бы этот вопрос увидели те кто действительно понимает ,просто мне очень нужно решение, спасибо за понимание!!!
Приложения:
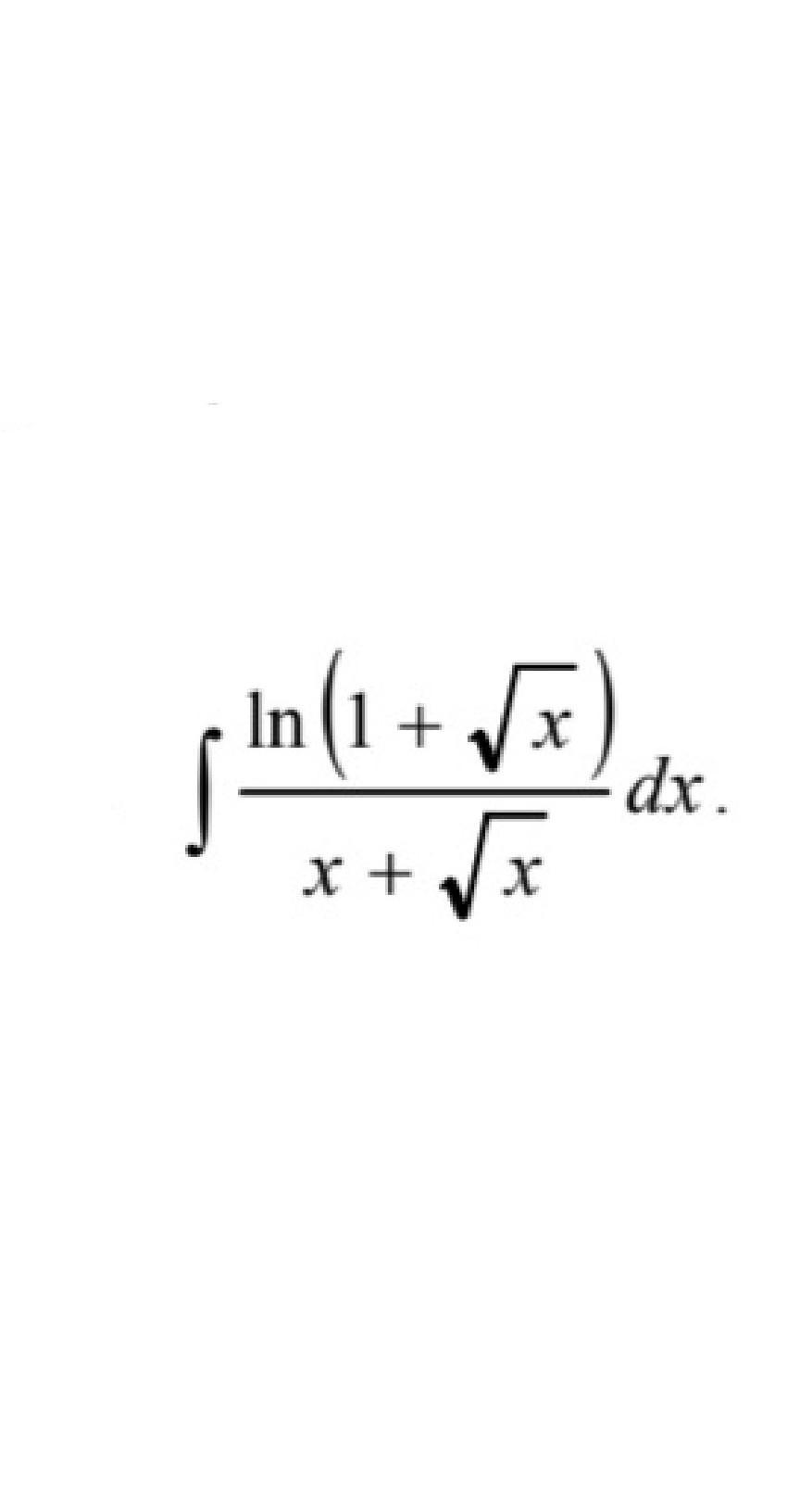
Ответы
Автор ответа:
1
Ответ:
Замена:
Замена:
undina77:
спасибо огромное, у меня есть 2 таких же вопроса в профиле по 10 баллов ставила, не могла вначале больше сделать, можете ответить это там если хотите
Да не нужно, спасибо)
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: данил00925367635
Предмет: Русский язык,
автор: ket57
Предмет: Русский язык,
автор: Ариза200405
Предмет: Английский язык,
автор: перизат23
Предмет: Английский язык,
автор: Xenia1111111