Предмет: Математика,
автор: nikirol228
Найти производные функции двух переменных.
dz/dx, если z=u*sin(uv), где u=y/x, v=x-y.
(141 номер задачи)
Приложения:
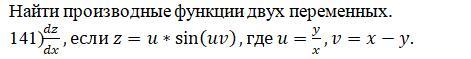
Ответы
Автор ответа:
1
Ответ:
Miroslava227:
В частных производных закругленная d
dz/du=(u*sin(uv) )^/=sin(uv)+u*cos(uv)*v
dz/dv=(u*sin(uv) )^/=0*sin(uv)+u*cos(uv)*u=u^2*cos(uv)
du/dx=〖(y/x)〗^/=(-y)/x^2
dv/dx=(x-y)^/=1-0=1
dz/dx=dz/du*du/dx+dz/dv*dv/dx=(sin(uv)+u*cos(uv)*v)*((-y)/x^2 )+u^2*cos(uv)*1=
=(-sin〖(uv)*y〗/x^2 -cos(uv)*(v*u*y)/x^2 )+u^2*cos〖(uv)=〗
=u*cos(uv)*(u-(v*y)/x^2 )-sin〖(uv)*y〗/x^2
Ответ: dz/dx=u*cos(uv)*(u-(v*y)/x^2 )-sin〖(uv)*y〗/x^2
dz/dv=(u*sin(uv) )^/=0*sin(uv)+u*cos(uv)*u=u^2*cos(uv)
du/dx=〖(y/x)〗^/=(-y)/x^2
dv/dx=(x-y)^/=1-0=1
dz/dx=dz/du*du/dx+dz/dv*dv/dx=(sin(uv)+u*cos(uv)*v)*((-y)/x^2 )+u^2*cos(uv)*1=
=(-sin〖(uv)*y〗/x^2 -cos(uv)*(v*u*y)/x^2 )+u^2*cos〖(uv)=〗
=u*cos(uv)*(u-(v*y)/x^2 )-sin〖(uv)*y〗/x^2
Ответ: dz/dx=u*cos(uv)*(u-(v*y)/x^2 )-sin〖(uv)*y〗/x^2
Похожие вопросы
Предмет: Русский язык,
автор: syuzannatamoya
Предмет: Русский язык,
автор: nhgjgjgbjtbjg8678475
Предмет: Немецкий язык,
автор: Мегамоозг
Предмет: Математика,
автор: danilivanov2021
Предмет: Биология,
автор: Liz05lll06