Question

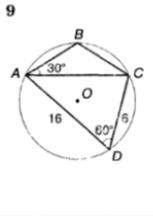
O-центр круга. Найти площадь ABCD.(100БАЛОВ)

Answer 1

Решение:

1) Р/м ΔDAC, АС²=16²+6²-2*16*6*cos60°

                      AC²=256+36-192 * 1/2

                      AC²=256+36-96

                      AC²=196

                      AC=14

2) Р/м ΔABC,

$\displaystyle \frac{14}{sim120} =\frac{BC}{sin30}$

$\displaystyle BC=\frac{14*\frac{1}{2} }{sin(180-120)}$

$\displaystyle BC=\frac{14*\frac{1}{2} }{\frac{\sqrt{3} }{2} }$

$\displaystyle BC=\frac{14}{\sqrt{3} }$

3) $\displaystyle Sabcd=\frac{1}{2} *AB*BC*sin120=\frac{1}{2} *\frac{14}{\sqrt{3} } *\frac{14}{\sqrt{3} } *\frac{\sqrt{3} }{2} =\frac{98\sqrt{3} }{3*2} =\frac{49\sqrt{3} }{3}$

4) $\displaystyle Sdac=\frac{1}{2} *16*6*sin60=48*sin60=48*\frac{\sqrt{3} }{2} =24\sqrt{3}$

5) $\displaystyle Sabcd=\frac{49\sqrt{3} }{3} +24\sqrt{3} =\frac{49\sqrt{3} +72\sqrt{3} }{3} =\frac{121\sqrt{3} }{3}$

Ответ: (121√3)/3

Answer 2

Так как в окружность вписан четырехугольник, то сумма противоположных углов составляет 180°, значит, ∠В=180°-∠D=180°-60°=

120°; а так как сумма углов в треугольнике АВС равна 180°, то ∠С=180°-30°-120°=30°⇒АВ=ВС.

Зная две стороны и угол между ними треугольника АСD, используя теорему косинусов, можно найти сторону АС.

АС=√(АD²+DC²-2AD*DC*cos60°)=√(16²+6²-2*6*16*0.5)=

√(256+36-96)=√196=14;

Найдем площадь треугольника АСD по формуле Герона.

Полупериметр равен (16+6+14)/2=18;  площадь равна

s=√(18*(18-6)(18-16)(18-14))=√(2*9*3*4*2*4)=3*2*4√3=24√3;

По теореме синусов из треугольника АВС

ВС/sin∠А=АС/sin∠B⇒ВС=AC*sin∠A/sin∠B=14*0.5*2/√3=14/√3=14√3/3; ВС=АВ=14√3/3;

Найдем площадь треугольника АСВ по формуле 0.5*АВ*АС*sin∠BAC=

0.5*0.5*14*14√3/3=49√3/3

Суммируя площади двух треугольников АВС и АDС, из которых состоит четырехугольник АВСD, получим искомую площадь: 24√3+49√3/3=121√3/3