Предмет: Геометрия,
автор: 602428272
помогите геометрия пожалуйста
Приложения:

Ответы
Автор ответа:
0
Угол между двумя прямыми - это угол между их направляющими векторами.
→s₁={6;5;-4}
→s₂={-1;-5;-2}
cosα=(s₁*s₂)/(Is₁I*Is₂I)=(6*(-1)+5*(-5)+(-4)*(-2))/(√(36+25+16)*√(1+25+4))=
(-6-25+8)/(√77*√30)=-23/√2310≈-23/48.062459363≈-0.4785
Автор ответа:
0
Ответ:
Объяснение:
В уравнении прямой
- координаты направляющего вектора.
Для прямой координаты направляющего вектора (6; 5; -4).
Для прямой координаты направляющего вектора (-1; -5; -2).
Угол между этими векторами равен углу между прямыми.
Из скалярного произведения векторов (см. фото) выражаем косинус угла.
Скалярное произведение векторов в прямоугольной системе координат вычисляется как сумма произведений соответствующих координат этих векторов.
→a*→b = 6*(-1)+5*(-5)+(-4)*(-2)= -6-25+8= -23
|→a| =
|→b| =
Приложения:
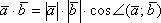
Похожие вопросы
Предмет: Английский язык,
автор: nastyakaiofjr
Предмет: Русский язык,
автор: Veronika350
Предмет: Русский язык,
автор: розочка4556
Предмет: Математика,
автор: ИвановаВалерия
Предмет: Русский язык,
автор: Saltaкласс