Question

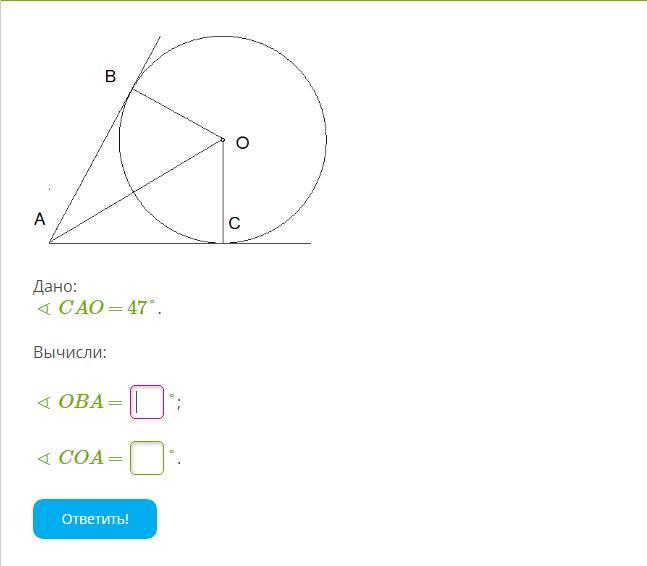
Дано:
∢ CAO = 47°.

Вычисли:

∢ OBA =
°;

∢ COA =
°.

Answer 1

Ответ:

Пошаговое объяснение:

∢ CAO = 47°.

Есть теоремы :

1)Две касательные ,проведенные из одной точки равны между собой.

2)Угол между радиусом в точку касания и касательной равен 90 °

АВ=АС  касательные из одной точки равны.

ОВ=ОС -радиусы. АО = АО

треугольники равны по трем сторонам. Значит и углы соответственно равны.  ∢ ВAO = 47°

Есть теоремы :

1)Две касательные ,проведенные из одной точки равны между собой.

2)Угол между радиусом в точку касания и касательной равен 90 °

∢ OBA = 90°  

∢ COA =  180-90-47=43° (из суммы углов треугольника =180°)