Question

Найдите объем правильной четырехугольной пирамиды, ребра которой равны 2 см . СРОЧНО ПРОШУ ВАС УМНЫЕ ЛЮДИ.

Answer 1

Ответ:

Объяснение:

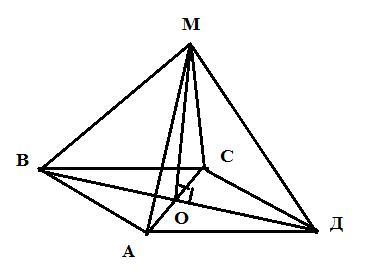
У правильной четырехугольной пирамиды в основании лежит квадрат.

У правильной пирамиды основание высоты падает в центр описанной окружности, значит равноудалено от вершин, следовательно падает на точку пересечения диагоналей.

Длина диагонали:

$BD=\sqrt{AB^2+AD^2} =\sqrt{2^2+2^2} =2\sqrt2}$ см

Тогда отрезок ОД в 2 раза меньше (так как диагонали квадрата в точке пересечения делятся пополам)

$OD = \sqrt{2}$

Тогда из прямоугольного треугольника МОД по Пифагору

$h=OM=\sqrt{MD^2-OD^2} = \sqrt{2^2-\sqrt{2}^2 } =\sqrt{2}$ см

Тогда объем пирамиды $V=\frac{1}{3} Sh = \frac{1}{3}AC*CD*h = \frac{1}{3} *2*2*\sqrt{2}= \frac{4}3} \sqrt{2}$