Помогите с алгеброй!!!
просьба не спамить!!!
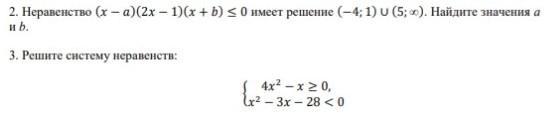
Ответы
Ответ:
В решении.
Объяснение:
Решить систему неравенств:
4х² - х >= 0
x² - 3x - 28 < 0
Решить первое неравенство:
4х² - х >= 0
Приравнять к нулю и решить как неполное квадратное уравнение:
4х² - х = 0
х(4х - 1) = 0
х₁ = 0;
4х - 1 = 0
4х = 1
х = 1/4
х₂ = 0,25.
Теперь начертить СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= 0 и х= 0,25, отметить эти точки схематично, смотрим на график.
По графику ясно видно, что у >= 0 (как в неравенстве) при х от - бесконечности до 0 и от 0,25 до + бесконечности.
Решение неравенства: х∈(-∞; 0]∪[0,25; +∞).
Неравенство нестрогое, скобки квадратные, а знаки бесконечности всегда с круглой скобкой.
Решить второе неравенство:
x² - 3x - 28 < 0
Приравнять к нулю и решить как квадратное уравнение:
x² - 3x - 28 = 0
D=b²-4ac = 9 + 112 = 121 √D=11
х₁=(-b-√D)/2a
х₁=(3-11)/2
х₁= -8/2
х₁= -4;
х₂=(-b+√D)/2a
х₂=(3+11)/2
х₂=14/2
х₂=7;
Теперь начертить СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -4 и х= 7, отметить эти точки схематично, смотрим на график.
По графику ясно видно, что у < 0 (как в неравенстве), при значениях х от -4 до х= 7.
Решение второго неравенства х∈(-4; 7).
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения - бесконечность, -4, 0, 0,25, 7, + бесконечность.
Решение первого неравенства: х∈(-∞; 0]∪[0,25; +∞). Штриховка от - бесконечности до 0 и от 0,25 до + бесконечности.
Решение второго неравенства: х∈(-4; 7). Штриховка от -4 до 7.
Двойная штриховка (пересечение решений) при х от -4 до х= 0 и при х от 0,25 до 7, это решение системы неравенств.
Запись: х∈(-4; 0]∪[0,25; 7). Точки у 0 и 0,25 закрашенные.
_______________________________________________________
-∞ -4 0 0,25 7 +∞
Примечание: определение решения неравенства при помощи параболы - вспомогательное действие, его записывать никуда не нужно. Записать: приравнять к нулю; решить уравнение и определить его корни; на черновике начертить схему графика; записать решение неравенства, отметить решение на числовой прямой.