Предмет: Алгебра,
автор: 00sabina0
помогите,дам 50 баллов
Приложения:
Ответы
Автор ответа:
1
Ответ:
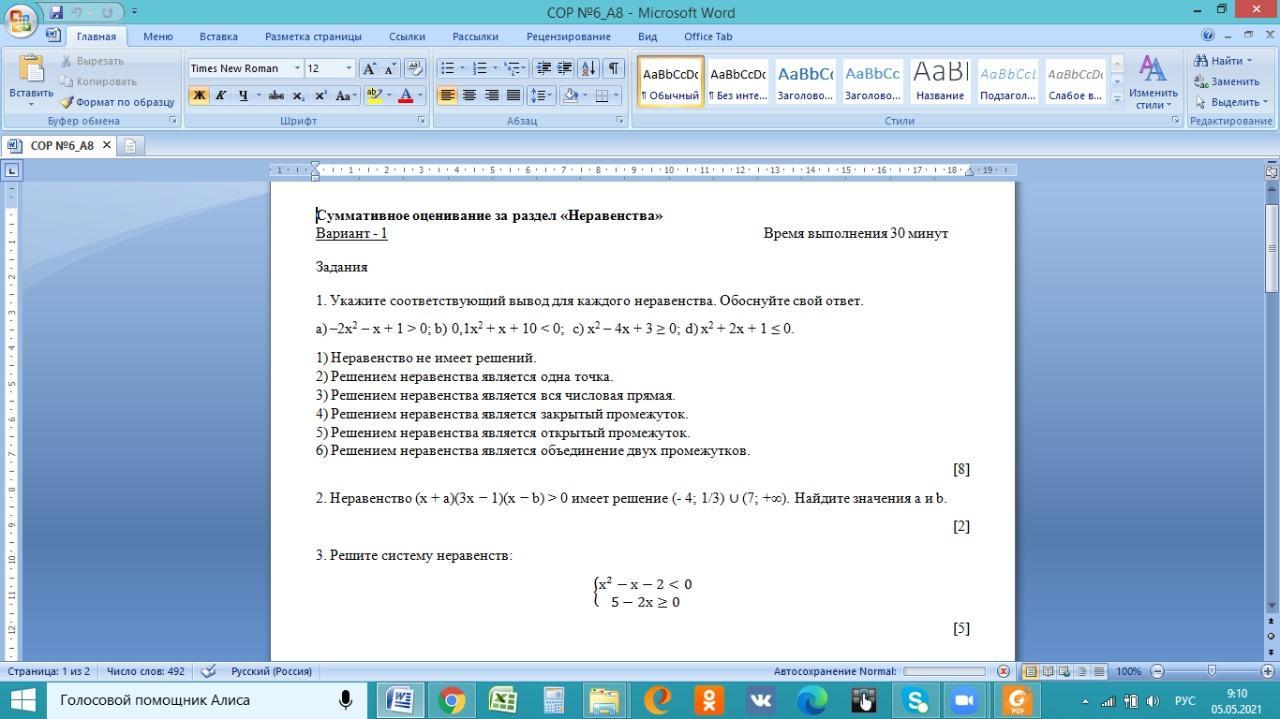
Ответ: №5 (открытый промежуток) .
Ответ: №1 (не имеет решений) .
Ответ: №6 (объединение двух промежутков) .
Ответ: №2 (одна точка) .
00sabina0:
спасибо,но уже поздно:)
Похожие вопросы
Предмет: Русский язык,
автор: 12345поо
Предмет: Французский язык,
автор: АняЛукина
Предмет: Русский язык,
автор: ангелинатаня
Предмет: Математика,
автор: 3627189
Предмет: Математика,
автор: tidjdjjffjjajd