Предмет: Математика,
автор: Бетси
Решииииите, одна задачка осталась. И я чем смогу помогу вам!!!!
Приложения:
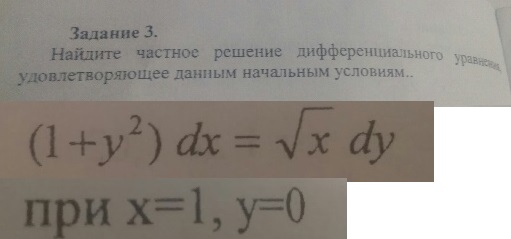
Ответы
Автор ответа:
0
Найдите частное решение диф. ур. с начальными условиями
(1+у²)dx =√(x)dy
при х=1,у=0
Решение
(1+у²)dx =√(x)dy
(1/(1+y²))dy =(1/√(x))dx
(1/(1+y²))dy =(x^(-1/2))dx
Интегрируем обе части уравнения
arctg(y) = 2x^(1/2) + C
arctg(y) = 2√(x) + C
Подставим начальные условия
arctg(0) = 2√(1) + C
С = -2
Запишем частное решений диф. ур.
arctg(y) = 2√(x) -2
или y = tg(2√(x) -2)
(1+у²)dx =√(x)dy
при х=1,у=0
Решение
(1+у²)dx =√(x)dy
(1/(1+y²))dy =(1/√(x))dx
(1/(1+y²))dy =(x^(-1/2))dx
Интегрируем обе части уравнения
arctg(y) = 2x^(1/2) + C
arctg(y) = 2√(x) + C
Подставим начальные условия
arctg(0) = 2√(1) + C
С = -2
Запишем частное решений диф. ур.
arctg(y) = 2√(x) -2
или y = tg(2√(x) -2)
Похожие вопросы
Предмет: Химия,
автор: karolina301106
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: rrrrr1eehehhe1
Предмет: Математика,
автор: veronika55555
Предмет: География,
автор: Kaifovaya