Предмет: Геометрия,
автор: nikita17157
Из центра окружности О к хорде AB, равной 30 см, проведен
перпендикуляр ОС. Найдите длину перпендикуляра, если АOВ=90
помогите пж пж пж с чертежом если можно
Ответы
Автор ответа:
2
Ответ:Если радиус окружности перпендикулярен к хорде,то он разделяет хорду пополам в точке их пересечения, т е АС=СВ
Соединим точки А и О,и О и В,получился равнобедренный треугольник
АО=ОВ , как радиусы,а значит
<А=<В=90:2=45
Перпендикуляр ОС не только высота,но и биссектриса(поделила угол 90 градусов пополам),но и медиана(разделила хорду на 2 равные части)
Перпендикуляр разделил треугольник АОВ на два прямоугольных равнобедренных треугольника АОС и СОВ
ОС=АС;ОС=СВ;
ОС=30:2=15 см
Объяснение:
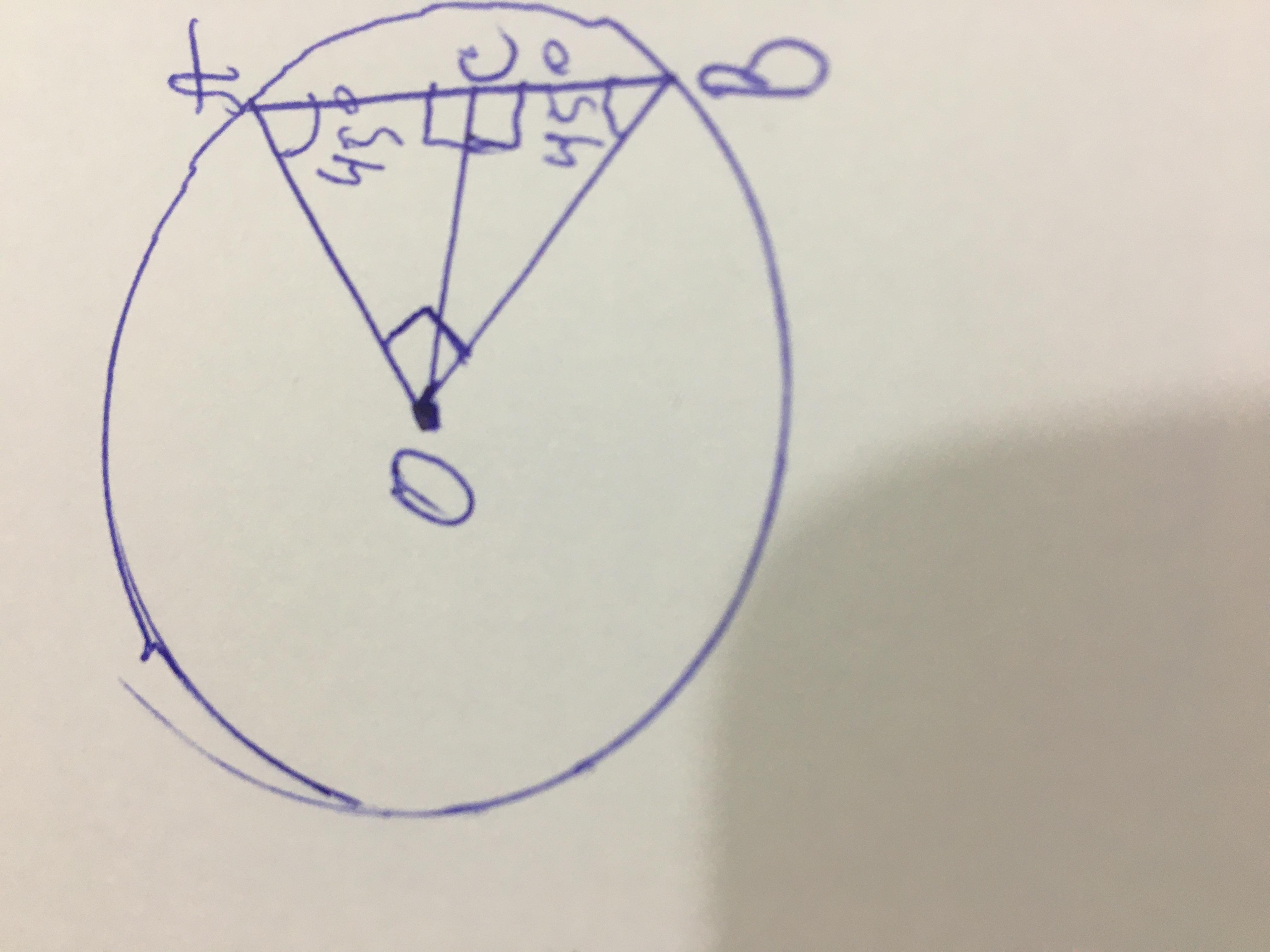
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: anna3Da5shaponeboga
Предмет: Русский язык,
автор: viplushkova
Предмет: Қазақ тiлi,
автор: Евангай
Предмет: Русский язык,
автор: moiseeva010
Предмет: Алгебра,
автор: Meggen