Предмет: Математика,
автор: Gestas
Помогите с дифф. уравнением, пожалуйста!
Приложения:
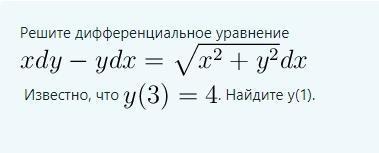
Ответы
Автор ответа:
0
Ответ: y+√(x²+y²)=C*x², y0²+√(x²+y0²)=x², y0(1)=0.
Пошаговое объяснение:
Разделив обе части уравнение на произведение x*dx, получим уравнение: dy/dx-y/x=√(1+y²/x²). Положим y/x=z ⇒ y=z*x ⇒ y'=dy/dx=z'*x+z и уравнение перепишется в виде: z'*x+z-z=√(1+z²), или z'*x=√(1+z²). А так как z'=dz/dx, то это уравнение приводится к виду dz/√(1+z²)=dx/x. Интегрируя, получаем: ln/z+√(1+z²)/=ln/x/+ln/C/, где C - произвольная, но не равная нулю, постоянная. Отсюда z+√(1+z²)=C*x. Заменяя z на y/x, находим y+√(x²+y²)=C*x². Используя условие y(3)=4, получаем уравнение 4+√25=9*C, откуда C=1 и тогда частное решение y0 удовлетворяет соотношению y0²+√(x²+y0²)=x². Подставляя в него значение x=1, приходим к уравнению y0²+√(1+y0²)=1. Решая его, находим y0=0.
Похожие вопросы
Предмет: Английский язык,
автор: Hahatushka11
Предмет: Немецкий язык,
автор: лейла61
Предмет: Русский язык,
автор: zhenykalinin200334
Предмет: Математика,
автор: МейблПайнс2005