Предмет: Алгебра,
автор: adultchild
определить независимое решение дифференциального уравнения:
y(0)=2;
y'(0)=0
Приложения:
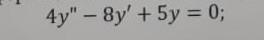
Ответы
Автор ответа:
1
Ответ:
общее решение
частное решение
Похожие вопросы
Предмет: Русский язык,
автор: maks510
Предмет: Русский язык,
автор: VadimZon
Предмет: Английский язык,
автор: R45245
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Окружающий мир,
автор: PinkPeach