Question

Вычислите площадь поверхности шара, описанного вокруг конуса, высота которого Н, а угол в осевом сечении конуса при вершине β.

Answer 1

Ответ:

Объяснение:

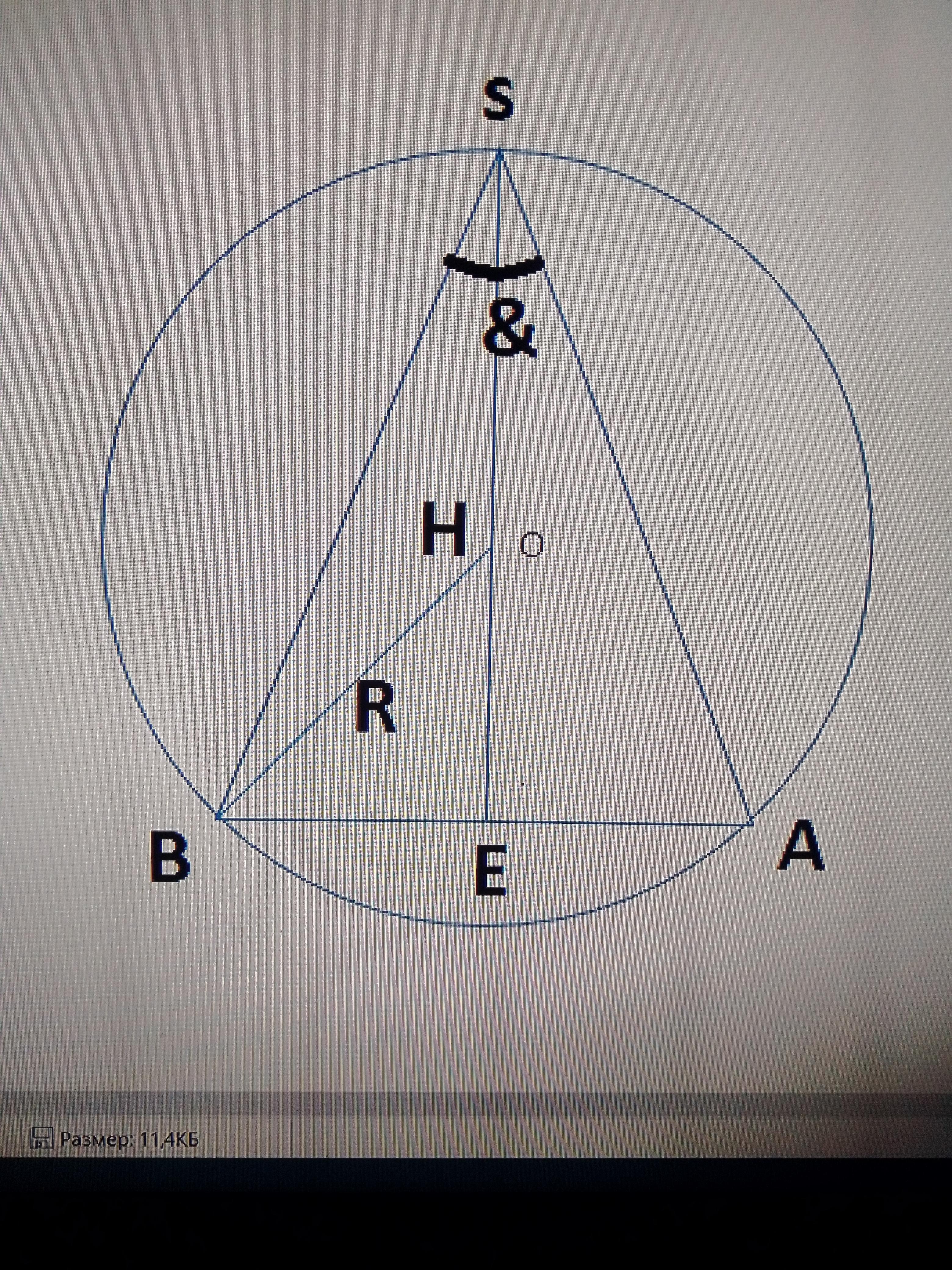
Дано: SHR - конус, Н - высота конуса, &- угол при вершине

OR - сфера описанная

Sш=?

Площадь поверхности шара определяется по формуле:

Sш=4π*R^2

В осевом сечении образуется равнобедренный ∆,

Центр окружности О лежит на высоте Н,

Cos(&/2) = H/SB;. SB=H/cos(&/2)

SB^2= 2R^2-2R^2*cos(180-&)

(H/cos(&/2))^2 =2R^2(1+cos&)

R^2=H^2/2cos[&/2]*2cos^2(&/2)

1+cos &= Cos^2(&/2)+sin^2(&/2)+

+cos^2(&/2)-sin^2(&/2)=2cos^2(&/2)

R^2=H^2/(4cos^3(&/2)

Sш=4πR^2

Sш=πН^2/(cos^3(&/2)