Предмет: Математика,
автор: rinnitan04200601
Пожалуйста помогите решить, буду очень благодарна. Дам 50 баллов
Приложения:
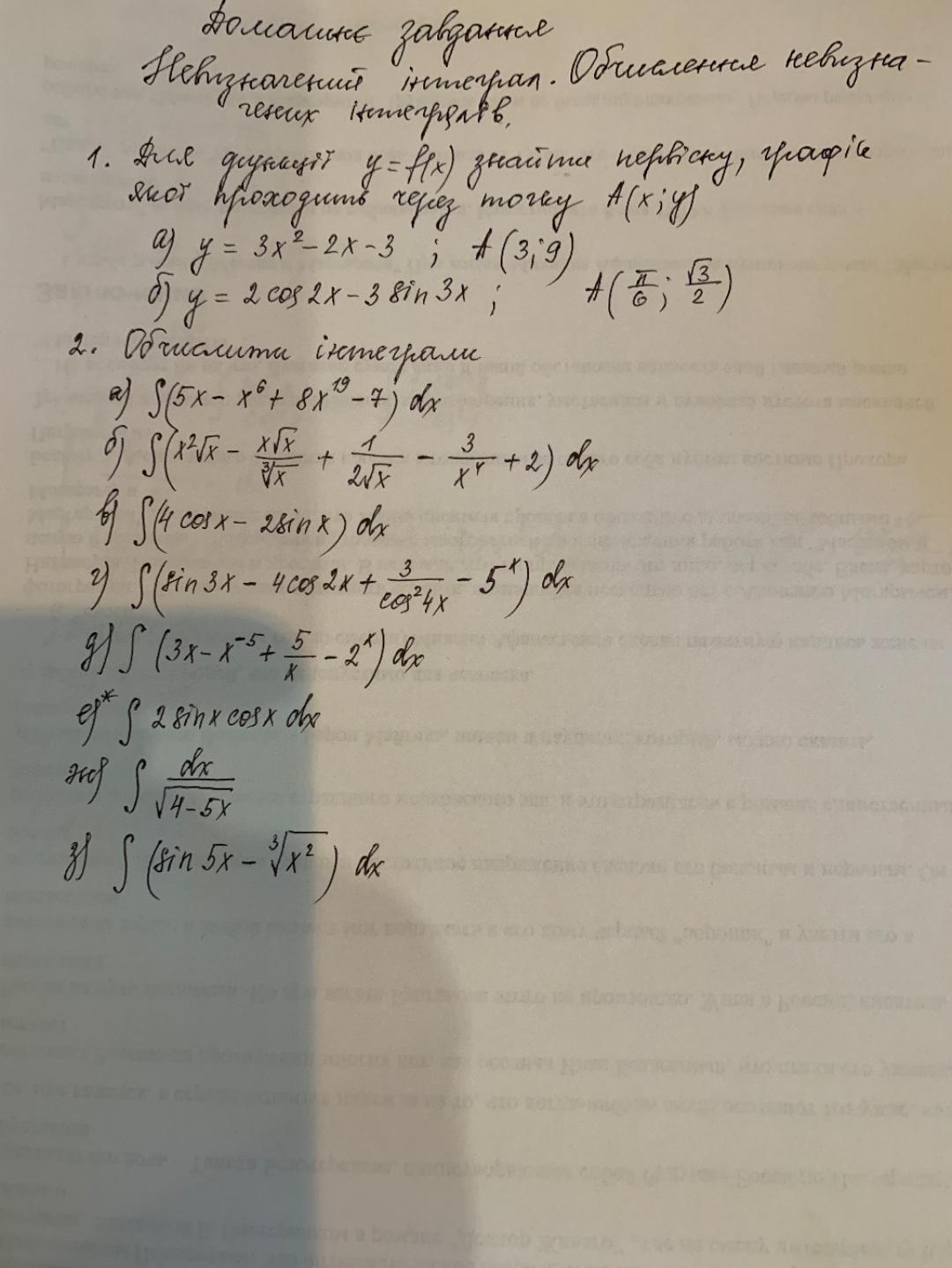
Ответы
Автор ответа:
1
Ответ:
1.
а
В точке А
б
В точке А
2.
а
б
в
г
д
е
ж
з
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: нюша9з
Предмет: Русский язык,
автор: амин13
Предмет: Математика,
автор: 1234567890870
Предмет: Русский язык,
автор: Crackstack18