Question

Через сторону АМ правильного треугольника АМВ проведена плоскость. Медиана ВD образует угол 60 градусов с плоскостью. Найти синус угла между прямой АВ и плоскостью.

Answer 1

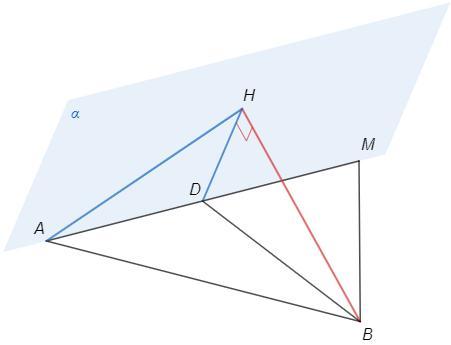
Через сторону треугольника проведена плоскость a.

Опустим перпендикуляр BH на плоскость a, BH⊥a

Угол между прямой и плоскостью - угол между прямой и ее проекцией.

∠BDH=60, ∠BAH - искомый угол

Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в плоскости.

∠BHD=∠BHA=90

Пусть AB=1

BD =AB sin(BAM) =√3/2

BH =BD sin(BDH) =√3/2 *√3/2 =3/4

sin(BAH) =BH/AB =3/4