1. Укажите область определения функции
2. Постройте график этой функции
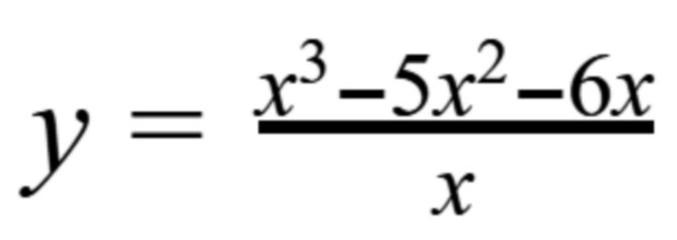
Ответы
Ответ:
В решении.
Объяснение:
1. Укажите область определения функции.
у = (х³ - 5х² - 6х)/х;
у = х(х² - 5х - 6)/х;
у = х² - 5х - 6;
График функции - парабола со смещённым центром.
Область определения функции - это значения х, при которых функция существует.
В данной функции по ОДЗ х не может быть равен 0.
А область определения параболы ничем не ограничена.
Поэтому область определения данной функции D(у)=х∈R : x≠0, то есть, функция определена при любом значении х, кроме х=0.
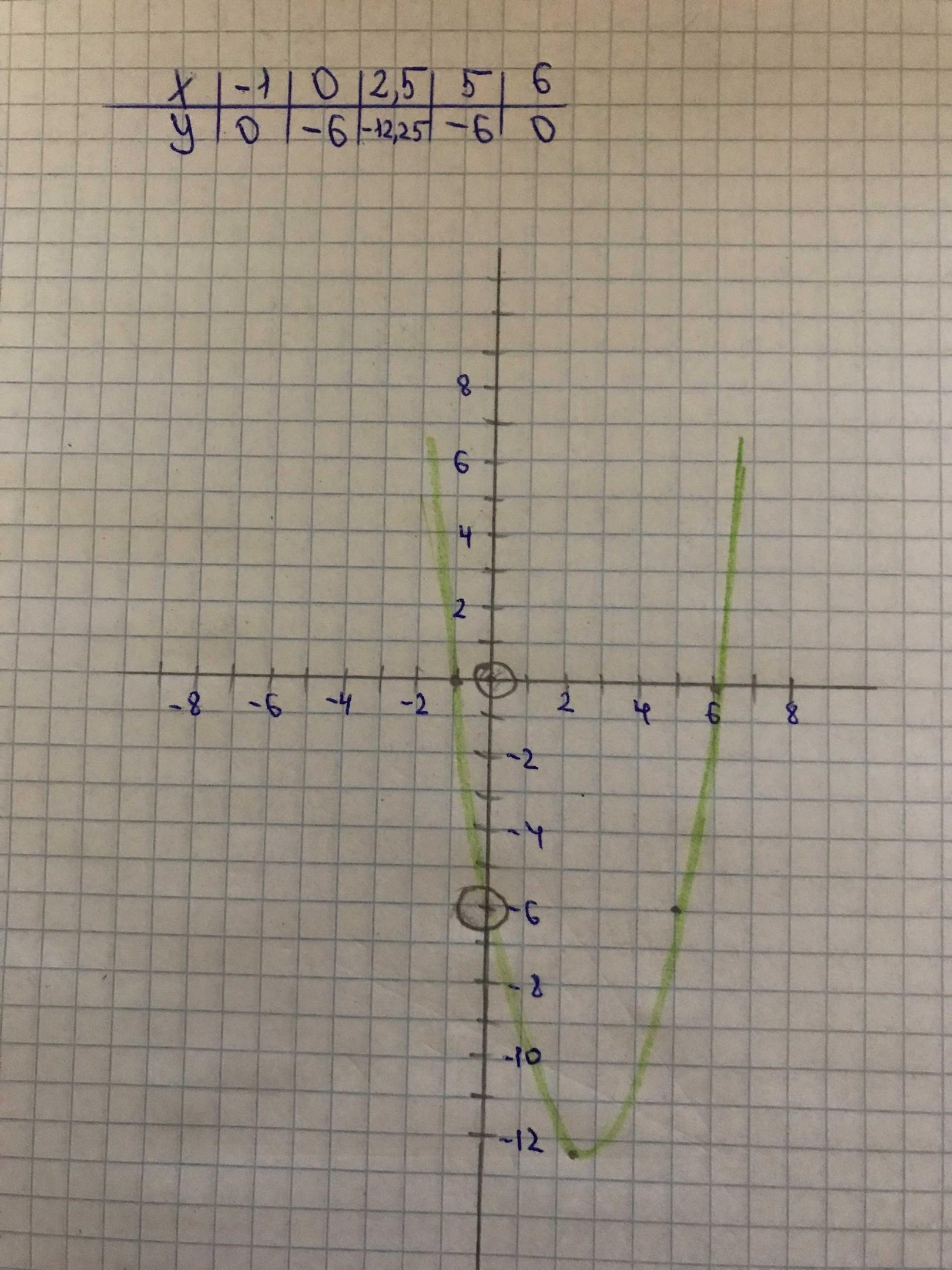
2. Постройте график этой функции.
y = x² - 5x - 6;
График - парабола со смещённым центром.
а) Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -5 0 5 10
у 44 -6 -6 44
б) Найти координаты вершины параболы:
х₀ = -b/2a
x₀ = 5/2 = 2,5;
у₀ = 2,5² -5*2,5 - 6 = 6,25 - 12,5 - 6 = -12,25;
Координаты вершины параболы (2,5; -12,25).
в) Найти нули функции (точки пересечения графиком оси Ох:
x² - 5x - 6 = 0
D=b²-4ac =25 + 24 = 49 √D=7
х₁=(-b-√D)/2a
х₁=(5-7)/2
х₁= -2/2
х₁= -1;
х₂=(-b+√D)/2a
х₂=(5+7)/2
х₂=12/2
х₂=6.
Координаты пересечения параболой оси Ох (-1; 0); (6; 0).
y=(x³-5x²-6x)/x
1) Функция определена, если x ≠ 0 , т.к делить на нуль нельзя, тогда функция примет вид:
y = x*(x²-5x-6)/x ;
y = x*(x²-5x-6)
y = x²-5x-6 ; x ≠ 0
xв = -b/2a = 5/2 = 2,5
yв = (5/2)² - 5 * 5/2 - 6 = 25/4 - 25/2 - 6 = (25-50-24)/4 = -49/4 = - 12,25
А ( 2,5 ; -12,25 ) - вершина