Предмет: Математика,
автор: niky21
Решайте следующий интеграл
Приложения:
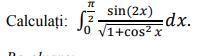
Ответы
Автор ответа:
1
Ответ: J=2*(√2-1).
Пошаговое объяснение:
Обозначим искомый интеграл через J. Замечая, что sin(2*x)=2*sin(x)*cos(x), cos²(x)=1-sin²(x) и cos(x)*dx=d[sin(x)], запишем соответствующий неопределённый интеграл в виде: F(x)=∫2*sin(x)*d[sin(x)]/√[2-sin²(x)]. Полагая sin(x)=u, получим F(u)=∫2*u*du/√(2-u²). Но так как d(2-u²)=-2*u*du, то F(u)=-∫d(2-u²)√(2-u²)=-∫(2-u²)^(-1/2)*d(2-u²). Интегрируя, находим F(u)=-2*√(2-u²). Отсюда F(x)=-2*√[2-sin²(x)], и тогда J=F(π/2)-F(0)=-2*√1+2*√2=2*√2-2=2*(√2-1).
Похожие вопросы
Предмет: Русский язык,
автор: конти3443
Предмет: Русский язык,
автор: eminsaruxanov
Предмет: Русский язык,
автор: sonop
Предмет: Математика,
автор: амка46368
Предмет: Қазақ тiлi,
автор: диана200614