Question

Найдите квадрат расстояния между серединами двух скрещивающихся ребер куба если этот куб вписан в Сферу поверхность которой равна 48 пи ​

Answer 1

Ответ:

24

Объяснение:

Формула площади сферы: S = 4πR²   R=D/2, S = πD², D - диаметр сферы.  πD²=48π ⇒ D=√48

Диаметр сферы, в который вписан куб - диагональ куба. Формула диагонали куба D=a√3 (можно найти по т. Пифагора) ⇒ сторона куба: а= D/√3 = √48/√3 = √16=4

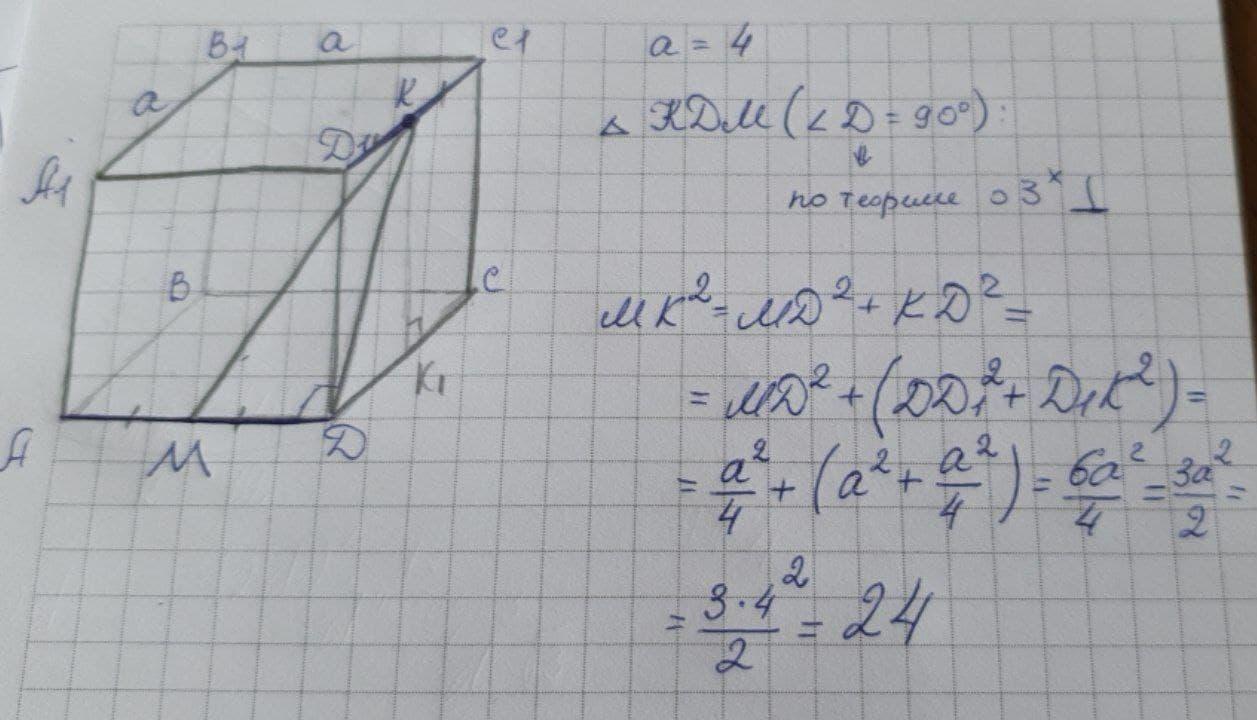
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. Рёбра Д1С1 и АД будут скрещивающиеся. Точки К и М - середины данных рёбер

Далее см. рисунок.

ΔКДМ: Проведём КК1 ║ С1С.

КК1 ⊥ДС, АД⊥ ДС ⇒

по теореме о 3 перпендикулярах  КД⊥АД ⇒ √Д=90°.